题目内容
设函数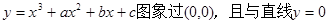 在原点相切,若函数的极小值为
在原点相切,若函数的极小值为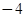 ;
;
(1)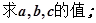
(2)求函数的递减区间。
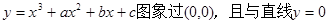 在原点相切,若函数的极小值为
在原点相切,若函数的极小值为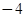 ;
;(1)
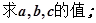
(2)求函数的递减区间。
(1)a=-3.(2)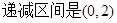
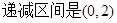
试题分析:(1)函数的图象经过(0,0)点,所以c=0,又图象与x轴相切于(0,0)点,
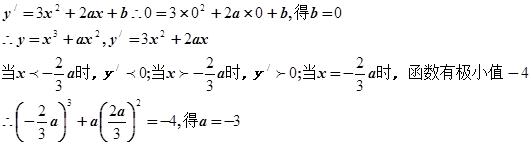
(2)

点评:典型题,应用“切线的斜率是函数在切点的导数值”求得b,确定得到函数解析式,通过“求导数、求驻点、解不等式、定导数符号”确定函数的单调区间及极值。

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
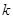 和
和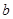 ,使得函数
,使得函数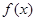 和
和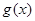 对其定义域上的任意实数
对其定义域上的任意实数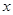 分别满足:
分别满足: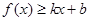 和
和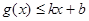 ,则称直线
,则称直线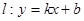 为
为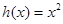 ,
,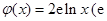 为自然对数的底数).
为自然对数的底数).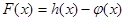 的极值;
的极值;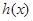 和
和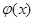 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.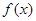 为定义在
为定义在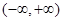 上的可导函数,且
上的可导函数,且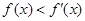 对于
对于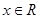 恒成立,且
恒成立,且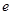 为自然对数的底,则( )
为自然对数的底,则( )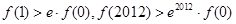
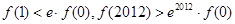
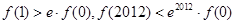
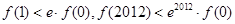
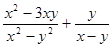 有意义的(x,y)出现的概率;
有意义的(x,y)出现的概率;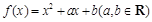 ,
,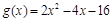 ,且
,且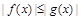 对
对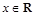 恒成立.
恒成立.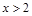 ,不等式
,不等式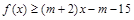 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.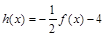 ,那么当
,那么当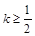 时,是否存在区间
时,是否存在区间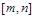 (
(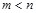 ),使得函数
),使得函数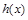 在区间
在区间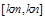 ?若存在,请求出区间
?若存在,请求出区间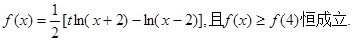
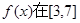 上取得最大值;
上取得最大值;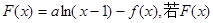 是单调递增函数,求a的取值范围.
是单调递增函数,求a的取值范围.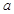 元(
元(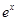 (e为自然对数的底数)成反比例。已知每件产品的日售价为40元时,日销售量为10件。
(e为自然对数的底数)成反比例。已知每件产品的日售价为40元时,日销售量为10件。
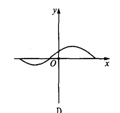

 的单调区间和值域。
的单调区间和值域。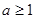 ,求函数
,求函数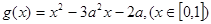 ,若对于任意
,若对于任意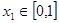 ,总存在
,总存在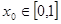 ,使得
,使得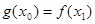 成立,求实数
成立,求实数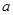 的取值范围。
的取值范围。