题目内容
【题目】如图,已知四边形![]() 为菱形,且
为菱形,且![]() ,取
,取![]() 中点为
中点为![]() .现将四边形
.现将四边形![]() 沿
沿![]() 折起至
折起至![]() ,使得
,使得![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)若点![]() 满足
满足![]() ,当
,当![]() 平面
平面![]() 时,求
时,求![]() 的值.
的值.
【答案】(Ⅰ)见解析;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(Ⅰ)只需证明![]() ,
,![]() ,
,![]() ,由线面垂直的判定定理可得证明;
,由线面垂直的判定定理可得证明;
(Ⅱ)以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系,求得平面
轴建立空间直角坐标系,求得平面![]() 的法向量和平面
的法向量和平面![]() 的法向量.设二面角
的法向量.设二面角![]() 的大小为
的大小为![]() ,可知
,可知![]() 为锐角,利用空间向量法即可得到所求值;
为锐角,利用空间向量法即可得到所求值;
(Ⅲ)由![]() 计算出向量
计算出向量![]() 的坐标,由
的坐标,由![]() ,计算可得所求值.
,计算可得所求值.
(Ⅰ)在左图中,![]() 为等边三角形,E为
为等边三角形,E为![]() 中点,所以
中点,所以![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ;
;
(Ⅱ)设菱形![]() 的边长为
的边长为![]() ,由(Ⅰ)可知
,由(Ⅰ)可知![]() ,
,![]() ,
,![]() .
.
所以以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴,建立如图空间坐标系.
轴,建立如图空间坐标系.
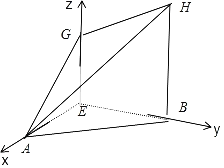
可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,所以
,所以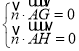 ,即
,即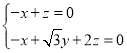 .
.
令![]() ,则
,则![]() .
.
平面![]() 的法向量为
的法向量为![]() .
.
设二面角![]() 的大小为
的大小为![]() ,则
,则![]() 为锐角,
为锐角,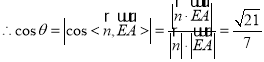 ;
;
(Ⅲ)由![]() ,
,![]()
因为![]() 平面
平面![]() ,则
,则![]() ,即
,即![]() ,所以
,所以![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为了比较两种治疗失眠症的药(分别称为![]() 药,
药,![]() 药)的疗效,某机构随机地选取
药)的疗效,某机构随机地选取![]() 位患者服用
位患者服用![]() 药,
药,![]() 位患者服用
位患者服用![]() 药,观察这
药,观察这![]() 位患者的睡眠改善情况.这些患者服用一段时间后,根据患者的日平均增加睡眠时间(单位:
位患者的睡眠改善情况.这些患者服用一段时间后,根据患者的日平均增加睡眠时间(单位:![]() ),以整数部分当茎,小数部分当叶,绘制了如下茎叶图:
),以整数部分当茎,小数部分当叶,绘制了如下茎叶图:
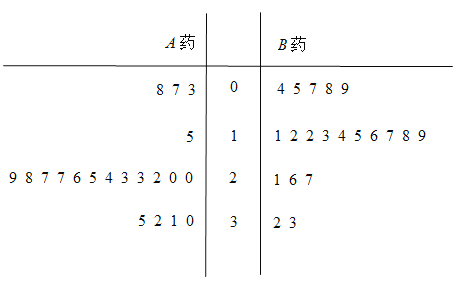
(1)根据茎叶图判断哪种药对增加睡眠时间更有效?并说明理由;
(2)求这![]() 名患者日平均增加睡眠时间的中位数
名患者日平均增加睡眠时间的中位数![]() ,并将日平均增加睡眠时间超过
,并将日平均增加睡眠时间超过![]() 和不超过
和不超过![]() 的患者人数填入下面的列联表:
的患者人数填入下面的列联表:
超过 | 不超过 | |
服用 | ||
服用 |
(3)根据(2)中的列联表,能否有![]() 的把握认为
的把握认为![]() 两种药的疗效有差异?
两种药的疗效有差异?
附: 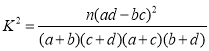 .
.
| 0.01 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |