题目内容
【题目】已知![]() 为实数,用
为实数,用![]() 表示不超过
表示不超过![]() 的最大整数,例如
的最大整数,例如![]() ,
,![]() ,
,![]() ,对于函数
,对于函数![]() ,若存在
,若存在![]() ,
,![]() ,使得
,使得![]() ,则称函数
,则称函数![]() 是“
是“![]() 函数”.
函数”.
(1)判断函数![]() ,
,![]() 是否是“
是否是“![]() 函数”;
函数”;
(2)设函数![]() 是定义在
是定义在![]() 上的周期函数,其最小正周期是
上的周期函数,其最小正周期是![]() ,若
,若![]() 不是“
不是“![]() 函数”,求
函数”,求![]() 的最小值;
的最小值;
(3)若函数![]() 是“
是“![]() 函数”,求
函数”,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 是,
是,![]() 不是;(2)1;(3)
不是;(2)1;(3)![]() ,且
,且![]() ,
,![]() .
.
【解析】
(1)举例说明函数![]() 是
是![]() 函数,证明函数
函数,证明函数![]() 不是“
不是“![]() 函数”;
函数”;
(2)假设![]() ,得到矛盾,再证明
,得到矛盾,再证明![]() 得证;
得证;
(3)对![]() 分
分![]() 三种情况讨论得解.
三种情况讨论得解.
(1)对于函数![]() 是
是![]() 函数,设
函数,设![]() ,
,![]()
则![]() ,
,![]() ,
,
所以存在![]() ,
,![]() ,使得
,使得![]() ,所以函数
,所以函数![]() 是“
是“![]() 函数”.
函数”.
对于函数![]() ,函数的最小正周期为
,函数的最小正周期为![]() ,函数的图象如图所示,
,函数的图象如图所示,
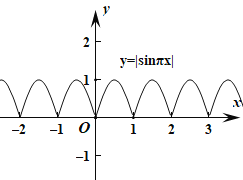
不妨研究函数在[0,1]这个周期的图象.
设![]() ,
,![]() ,则
,则![]() ,
,
所以![]() ,
,
所以函数![]() 不是“
不是“![]() 函数”.
函数”.
综合得函数![]() 是“
是“![]() 函数”,函数
函数”,函数![]() 不是“
不是“![]() 函数”.
函数”.
(2)![]() 的最小值为1.
的最小值为1.
因为![]() 是以
是以![]() 为最小正周期的周期函数,所以
为最小正周期的周期函数,所以![]() .
.
假设![]() ,则
,则![]() ,所以
,所以![]() ,矛盾.
,矛盾.
所以必有![]() .
.
而函数![]() 的周期为1,且显然不是
的周期为1,且显然不是![]() 函数,
函数,
综上所述,![]() 的最小值为1.
的最小值为1.
(3)当函数![]() 是“
是“![]() 函数”时,
函数”时,
若![]() ,则
,则![]() 显然不是
显然不是![]() 函数,矛盾.
函数,矛盾.
若![]() ,则
,则![]() ,
,
所以![]() 在
在![]() ,
,![]() 上单调递增,
上单调递增,
此时不存在![]() ,使得
,使得![]() ,
,
同理不存在![]() ,使得
,使得![]() ,
,
又注意到![]() ,即不会出现
,即不会出现![]() 的情形,
的情形,
所以此时![]() 不是
不是![]() 函数.
函数.
当![]() 时,设
时,设![]() ,所以
,所以![]() ,
,
所以有![]() ,其中
,其中![]() ,
,
当![]() 时,
时,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
综上所述,![]() ,且
,且![]() ,
,![]() .
.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目