题目内容
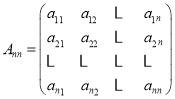
【题目】以直角坐标系![]() 的原点为极点,x轴的非负半轴为极轴建立极坐标系,并且在两种坐标系中取相同的长度单位.若将曲线
的原点为极点,x轴的非负半轴为极轴建立极坐标系,并且在两种坐标系中取相同的长度单位.若将曲线![]() (
(![]() 为参数)上每一点的横坐标变为原来的
为参数)上每一点的横坐标变为原来的![]() (纵坐标不变),然后将所得图象向右平移2个单位,再向上平移3个单位得到曲线C.直线l的极坐标方程为
(纵坐标不变),然后将所得图象向右平移2个单位,再向上平移3个单位得到曲线C.直线l的极坐标方程为![]() .
.
(1)求曲线C的普通方程;
(2)设直线l与曲线C交于A,B两点,与x轴交于点P,线段AB的中点为M,求![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据题意得到![]() (
(![]() 为参数)后,消去参数
为参数)后,消去参数![]() 即可得到曲线C的普通方程;
即可得到曲线C的普通方程;
(2)将直线![]() 的方程化为参数方程的标准形式并代入到圆
的方程化为参数方程的标准形式并代入到圆![]() 的方程,利用参数的几何意义可解得结果.
的方程,利用参数的几何意义可解得结果.
(1)将曲线![]() (
(![]() 为参数)上每一点的横坐标变为原来的
为参数)上每一点的横坐标变为原来的![]() (纵坐标不变),得到
(纵坐标不变),得到![]() , 然后将所得图像向右平移2个单位,再向上平移3个单位得到
, 然后将所得图像向右平移2个单位,再向上平移3个单位得到![]() (
(![]() 为参数),消去参数
为参数),消去参数![]() 得圆C的普通方程为
得圆C的普通方程为![]() .
.
(2)由![]() 得
得![]() ,即
,即![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
即直线l的直角坐标方程为:![]() ,倾斜角为
,倾斜角为![]() ,点
,点![]() ,
,
设直线l的参数方程为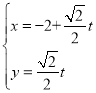 ,代入圆C的普通方程
,代入圆C的普通方程![]() 并整理得:
并整理得:![]() ,
,
因为![]() ,设
,设![]() 、
、![]() 两点对应的参数分别为
两点对应的参数分别为![]() ,
,![]() ,则
,则![]() 点对应的参数为
点对应的参数为![]() ,
,
由韦达定理得![]() ,
,![]() ,
,
则![]() .
.

【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在![]() 实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图,记综合评分为80分及以上的花苗为优质花苗.
实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图,记综合评分为80分及以上的花苗为优质花苗.
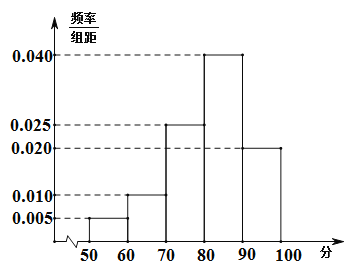
(1)用样本估计总体,以频率作为概率,若在![]() 两块实验地随机抽取3株花苗,求所抽取的花苗中优质花苗数的分布列和数学期望;
两块实验地随机抽取3株花苗,求所抽取的花苗中优质花苗数的分布列和数学期望;
(2)填写下面的列联表,并判断是否有99%的把握认为优质花苗与培育方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合计 |
附:下面的临界值表仅供参考.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(参考公式: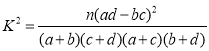 ,其中
,其中![]() )
)
【题目】下表为![]() 年至
年至![]() 年某百货零售企业的线下销售额(单位:万元),其中年份代码
年某百货零售企业的线下销售额(单位:万元),其中年份代码![]() 年份
年份![]() .
.
年份代码 |
|
|
|
|
线下销售额 |
|
|
|
|
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 年该百货零售企业的线下销售额;
年该百货零售企业的线下销售额;
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了![]() 位男顾客、
位男顾客、![]() 位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有
位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有![]() 人、女顾客有
人、女顾客有![]() 人,能否在犯错误的概率不超过
人,能否在犯错误的概率不超过![]() 的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
参考公式及数据: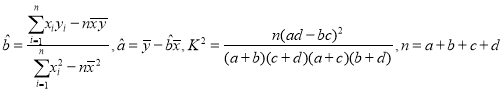 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|