题目内容
16.某人在C点测得某塔在南偏西80°,塔顶仰角为45°,此人沿南偏东40°方向前进10米到D点测得塔顶A的仰角为30°,则塔高为( )| A. | 15米 | B. | 5米 | C. | 10米 | D. | 12米 |
分析 先设出塔高为h,进而在Rt△AOC中求得OC=OA,在Rt△AOD中根据∠ADO=30°表示出OD最后在△OCD中,利用余弦定理求得关于h的一元二次方程进而求得h
解答 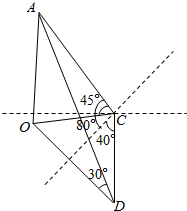 解:如图,
解:如图,
设塔高为h,
在Rt△AOC中,∠ACO=45°,
则OC=OA=h.
在Rt△AOD中,
∠ADO=30°,则OD=$\sqrt{3}$h,
在△OCD中,
∠OCD=120°,CD=10,
由余弦定理得:OD2=OC2+CD2-2OC•CDcos∠OCD,
即($\sqrt{3}$h)2=h2+102-2h×10×cos120°,
∴h2-5h-50=0,解得h=10或h=-5(舍);
故选C.
点评 本题主要考查了解三角形的实际应用.关键是将实际问题转化为解三角形的问题解答;考查了学生综合分析问题和解决问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.当-π≤x≤0时,函数$f(x)=sinx+\sqrt{3}cosx$最小值为( )
| A. | -1 | B. | -2 | C. | $-\sqrt{3}$ | D. | 0 |
4.设t是函数f(x)=ex+lnx的零点,若x0>t,则f(x0)的值满足( )
| A. | f(x0)=0 | B. | f(x0)>0 | C. | f(x0)<0 | D. | f(x0)的符号不确定 |
9.若$\sqrt{\frac{1+sinα}{1-sinα}}$-$\sqrt{\frac{1-sinα}{1+sinα}}$=2tanα恒成立,则角α可能在的象限是( )
| A. | 第一象限 | B. | 第四象限 | C. | 第一、四象限 | D. | 第二、三象限 |
 如图,在平面直角坐标系中,锐角a、β的终边分别与单位圆交于A、B两点.
如图,在平面直角坐标系中,锐角a、β的终边分别与单位圆交于A、B两点.