题目内容
设数列{an}的首项不为零,前n项和为Sn,且对任意的r,t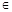 N*,都有
N*,都有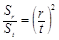 .
.
(1)求数列{an}的通项公式(用a1表示);
(2)设a1=1,b1=3,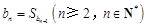 ,求证:数列
,求证:数列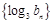 为等比数列;
为等比数列;
(3)在(2)的条件下,求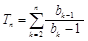 .
.
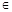 N*,都有
N*,都有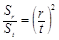 .
.(1)求数列{an}的通项公式(用a1表示);
(2)设a1=1,b1=3,
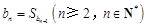 ,求证:数列
,求证:数列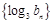 为等比数列;
为等比数列;(3)在(2)的条件下,求
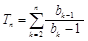 .
.(1) ;(2)详见解析;(3)
;(2)详见解析;(3) .
.
 ;(2)详见解析;(3)
;(2)详见解析;(3) .
.试题分析:(1)根据题中所给数列递推关系的特征:
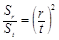 ,有且只有前n项和的比值,而题中又要求以a1表示,即可想到令
,有且只有前n项和的比值,而题中又要求以a1表示,即可想到令 ,
, ,得到
,得到 ,这样问题即可转化为由
,这样问题即可转化为由 求
求 的问题,注意要分三步啊; (2)由(1)中所求
的问题,注意要分三步啊; (2)由(1)中所求 的表达式,并已知a1=1,即可确定出
的表达式,并已知a1=1,即可确定出 的通项公式和前n项和公式,再运用条件
的通项公式和前n项和公式,再运用条件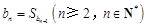 ,不难求出关系:
,不难求出关系: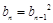 ,结合所证数列的特征和等比数列的定义,可得
,结合所证数列的特征和等比数列的定义,可得 ,即可得证;(3)由在(2)的条件下,即可得出
,即可得证;(3)由在(2)的条件下,即可得出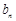 的通项公式:
的通项公式: 化简得
化简得 ,观察其特点和所求目标
,观察其特点和所求目标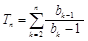 ,不难想到求出:
,不难想到求出: ,运用代数知识化简得:
,运用代数知识化简得: ,这样就可联想到数列求和中的裂项相消的方法,可得:
,这样就可联想到数列求和中的裂项相消的方法,可得: .
.试题解析:(1)因为
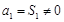 ,令
,令 ,
, ,则
,则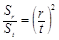 ,得
,得 ,即
,即 . 2分
. 2分当
 时,
时, ,且当
,且当 时,此式也成立.
时,此式也成立.故数列{an}的通项公式为
 . 5分
. 5分(2)当
 时,由(1)知
时,由(1)知 ,Sn=n2.
,Sn=n2.依题意,
 时,
时,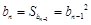 , 7分
, 7分于是
 ,且
,且 ,
,故数列
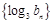 是首项为1,公比为2的等比数列. 10分
是首项为1,公比为2的等比数列. 10分(3)由(2)得
 ,所以
,所以 . 12分
. 12分于是
 . 15分
. 15分所以
 . 16分
. 16分
练习册系列答案
相关题目
 中,
中,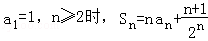
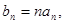 求数列
求数列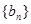 的前n项和Tn.
的前n项和Tn. ,都有
,都有
 .
. ,试探究:数列{bn}中是否存在某一项,它可以表示为该数列中其它
,试探究:数列{bn}中是否存在某一项,它可以表示为该数列中其它 项的和?若存在,请求出该项;若不存在,请说明理由.
项的和?若存在,请求出该项;若不存在,请说明理由.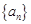 中,已知
中,已知 ,
, .设
.设 为该数列的前
为该数列的前 项和,
项和, 为数列
为数列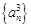 的前
的前 项和.若
项和.若 ,则实数
,则实数 的值为 .
的值为 .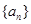 是首项为
是首项为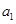 ,公差为
,公差为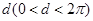 的等差数列,若数列
的等差数列,若数列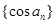 是等比数列,则其公比为( )
是等比数列,则其公比为( )


 中,
中,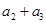 =1,
=1,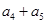 =2,则
=2,则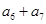 等于( ).
等于( ).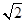
 -
- +
+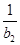 +…+
+…+ ,求T2012;
,求T2012; 中,
中, 前三项和为S3=27,则公比q的值是( )
前三项和为S3=27,则公比q的值是( )
 的前
的前 项和为
项和为 ,且
,且 ,
, ,
, 成等差数列,则数列
成等差数列,则数列