题目内容
若函数f(n)= ,an=f(n)+f(n+1),则a1+a2+a3+…+a2012=
,an=f(n)+f(n+1),则a1+a2+a3+…+a2012=
 ,an=f(n)+f(n+1),则a1+a2+a3+…+a2012=
,an=f(n)+f(n+1),则a1+a2+a3+…+a2012=| A.-1 | B.0 | C.1 | D.2 |
B
此题答案应选B
分析:由已知可得,当n为奇数时,an=f(n)+f(n+1)=n-(n+1)=-1;当n为偶数时,an=f(n)+f(n+1)=-n+(n+1)=1,而a1+a2+a3+…+a2012=(a1+a3+…+a2011)+(a2+a4+…+a2012),代入可求
解答:解:∵f(n)=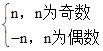
∵an=f(n)+f(n+1)
当n为奇数时,an=f(n)+f(n+1)=n-(n+1)=-1
当n为偶数时,an=f(n)+f(n+1)=-n+(n+1)=1
∴a1+a2+a3+…+a2012
=(a1+a3+…+a2011)+(a2+a4+…+a2012)
=1006×(-1)+1006×1=0
故选B
分析:由已知可得,当n为奇数时,an=f(n)+f(n+1)=n-(n+1)=-1;当n为偶数时,an=f(n)+f(n+1)=-n+(n+1)=1,而a1+a2+a3+…+a2012=(a1+a3+…+a2011)+(a2+a4+…+a2012),代入可求
解答:解:∵f(n)=
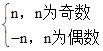
∵an=f(n)+f(n+1)
当n为奇数时,an=f(n)+f(n+1)=n-(n+1)=-1
当n为偶数时,an=f(n)+f(n+1)=-n+(n+1)=1
∴a1+a2+a3+…+a2012
=(a1+a3+…+a2011)+(a2+a4+…+a2012)
=1006×(-1)+1006×1=0
故选B

练习册系列答案
相关题目
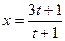 。已知2010年生产饮料的设备折旧
。已知2010年生产饮料的设备折旧 ,维修等固定费用为3 万元,每生产1万件
,维修等固定费用为3 万元,每生产1万件 成本—促销费,生产成本=固定费用+生产费用)
成本—促销费,生产成本=固定费用+生产费用)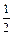 时,该商品的价格上涨多少,就能使销售的总金额最大?
时,该商品的价格上涨多少,就能使销售的总金额最大?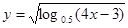 的定义域是 ( )
的定义域是 ( )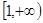
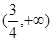
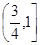
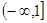
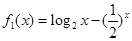 ,
,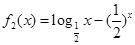 的零点分别为
的零点分别为 ,则( )
,则( )
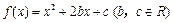 ,且
,且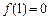 .
.
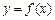 与x轴的两个交点
与x轴的两个交点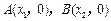 之间的距离为2,求b的值;
之间的距离为2,求b的值; 方程
方程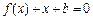 的两个实数根分别在区间
的两个实数根分别在区间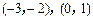 内,求b的取值范
内,求b的取值范 围.
围.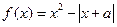 为偶函数,则实数
为偶函数,则实数
 [
[