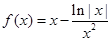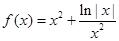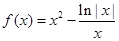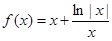题目内容
(本小题满分12分)已知某商品的价格上涨x%,销售的数量就减少mx%,其中m为正的常数。
(1)当m=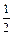 时,该商品的价格上涨多少,就能使销售的总金额最大?
时,该商品的价格上涨多少,就能使销售的总金额最大?
(2)如果适当地涨价,能使销售总金额增加,求m的取值范围
(1)当m=
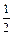 时,该商品的价格上涨多少,就能使销售的总金额最大?
时,该商品的价格上涨多少,就能使销售的总金额最大?(2)如果适当地涨价,能使销售总金额增加,求m的取值范围
解:(1)设商品现在定价a元,卖出的数量为b个。
由题设:当价格上涨x%时,销售总额为y=a(1+x%)b(1-mx%),
即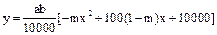 ,(0<x<
,(0<x<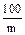 ),
),
取m=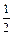 得:y=
得:y=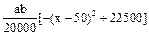 ,当x=50时,ymax=
,当x=50时,ymax=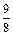 ab,
ab,
即:该商品的价格上涨50%时,销售总金额最大。
(2)二次函数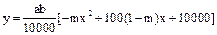 ,在
,在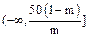 上递增,
上递增,
在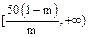 上递减,
上递减,
适当地涨价能使销售总金额增加,即 在(0,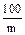 )内存在一个区间,使函数y在此区间上是
)内存在一个区间,使函数y在此区间上是
增函数,所以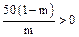 , 解得
, 解得 ,即所求
,即所求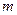 的取值范围是(0,1).
的取值范围是(0,1).
由题设:当价格上涨x%时,销售总额为y=a(1+x%)b(1-mx%),
即
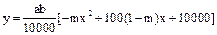 ,(0<x<
,(0<x<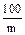 ),
),取m=
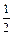 得:y=
得:y=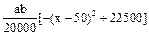 ,当x=50时,ymax=
,当x=50时,ymax=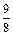 ab,
ab,即:该商品的价格上涨50%时,销售总金额最大。
(2)二次函数
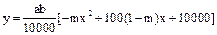 ,在
,在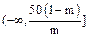 上递增,
上递增,在
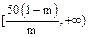 上递减,
上递减,适当地涨价能使销售总金额增加,即 在(0,
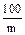 )内存在一个区间,使函数y在此区间上是
)内存在一个区间,使函数y在此区间上是增函数,所以
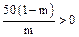 , 解得
, 解得 ,即所求
,即所求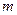 的取值范围是(0,1).
的取值范围是(0,1).略

练习册系列答案
相关题目
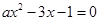 至少有一个负数根”的 ( ▲ )
至少有一个负数根”的 ( ▲ )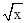 + 2x + log2x的值域是 {3,
+ 2x + log2x的值域是 {3, 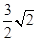 -1, 5 +
-1, 5 + 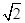 , 20},
, 20},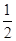 ,1,2,4}
,1,2,4}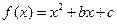 为偶函数,曲线
为偶函数,曲线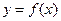 过点
过点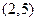 ,
,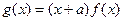 .
.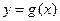 存在斜率为0的切线,求实数
存在斜率为0的切线,求实数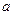 的取值范围;
的取值范围;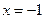 时函数
时函数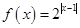 ,若
,若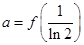 ,
,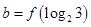 ,
,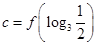 ,则
,则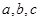 的大小关系是
的大小关系是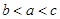
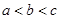
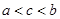
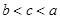
 ,an=f(n)+f(n+1),则a1+a2+a3+…+a2012=
,an=f(n)+f(n+1),则a1+a2+a3+…+a2012=
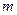 满足不等式
满足不等式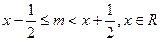 ,则称
,则称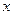 的“亲密整数”,记作
的“亲密整数”,记作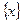 ,即
,即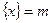 ,已知函数
,已知函数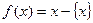 .给出以下四个命题:
.给出以下四个命题: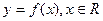 是周期函数且其最小正周期为
是周期函数且其最小正周期为 1;
1;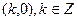 中心对称;
中心对称;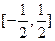 上单调递增;
上单调递增;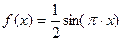 在
在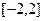 上共有7个不相等的实数根.
上共有7个不相等的实数根.
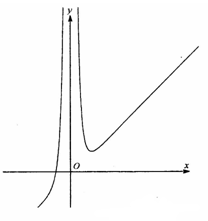
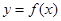 的大致图象如图所示,则函数
的大致图象如图所示,则函数