题目内容
已知函数y= sin(3x+
sin(3x+ )+1.
)+1.
(1)求y取最大值和最小值时相应的x的值;
(2)求函数的单调递增区间和单调递减区间;
(3)它的图象可以由正弦曲线经过怎样的图形变换所得出?
解:(1)由3x+ =2kπ+
=2kπ+ ,k∈z,可得x=
,k∈z,可得x= kπ+
kπ+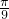 (k∈Z); 此时,y取最大值.
(k∈Z); 此时,y取最大值.
由3x+ =2kπ-
=2kπ- ,k∈z,可得x=
,k∈z,可得x= kπ-
kπ- ,(k∈Z),此时,y取最小值.
,(k∈Z),此时,y取最小值.
综上,可得y取最大值时,相应的x的值为x= kπ+
kπ+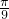 (k∈Z);y取最小值时,相应的x的值为x=
(k∈Z);y取最小值时,相应的x的值为x= kπ-
kπ- ,k∈Z.
,k∈Z.
(2)由 2kπ- ≤3x+
≤3x+ ≤2kπ+
≤2kπ+ ,k∈z,可得
,k∈z,可得  kπ-
kπ- ≤x≤
≤x≤ kπ+
kπ+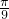 ,
,
故函数单调递增区间为[ kπ-
kπ- ,
, kπ+
kπ+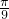 ](k∈Z).
](k∈Z).
由 2kπ+ ≤3x+
≤3x+ ≤2kπ+
≤2kπ+ ,k∈z,可得
,k∈z,可得  kπ+
kπ+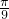 ≤x≤
≤x≤ kπ+
kπ+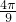 ,
,
故函数单调递减区间为[ kπ+
kπ+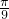 ,
, kπ+
kπ+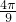 ](k∈Z);
](k∈Z);
(3)先将正弦曲线上每一点的横坐标变为原来的 (纵坐标不变),得到y=
(纵坐标不变),得到y= sin3x 的图象.
sin3x 的图象.
再将所得图象向左平移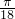 个单位,然后将所得图象上每一点的纵坐标变为原来的
个单位,然后将所得图象上每一点的纵坐标变为原来的 (横坐标不变),
(横坐标不变),
得到y= sin(3x+
sin(3x+ )的图象.
)的图象.
最后将所得图象向上平移一个单位,即可得到y= sin(3x+
sin(3x+ )+1的图象.
)+1的图象.
分析:(1)由3x+ =2kπ+
=2kπ+ ,k∈z,和 3x+
,k∈z,和 3x+ =2kπ-
=2kπ- ,k∈z,求得x的值,即为所求.
,k∈z,求得x的值,即为所求.
(2)由 2kπ- ≤3x+
≤3x+ ≤2kπ+
≤2kπ+ ,k∈z,求得x的范围,即得函数的增区间;由2kπ+
,k∈z,求得x的范围,即得函数的增区间;由2kπ+ ≤3x+
≤3x+ ≤2kπ+
≤2kπ+ ,
,
k∈z,求得x的范围,即得函数的减区间.
(3)先将y=sinx上每一点的横坐标变为原来的 ,再将所得图象向左平移
,再将所得图象向左平移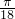 个单位,然后将所得图象上每一点的纵坐标变为原来的
个单位,然后将所得图象上每一点的纵坐标变为原来的 ,再把所得图象向上平移一个单位,即可得到y=
,再把所得图象向上平移一个单位,即可得到y= sin(3x+
sin(3x+ )+1的图象.
)+1的图象.
点评:本题主要考查y=Asin(ωx+∅)的图象变换,求三角函数的单调区间和最值的方法,属于中档题.
 =2kπ+
=2kπ+ ,k∈z,可得x=
,k∈z,可得x= kπ+
kπ+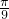 (k∈Z); 此时,y取最大值.
(k∈Z); 此时,y取最大值.由3x+
 =2kπ-
=2kπ- ,k∈z,可得x=
,k∈z,可得x= kπ-
kπ- ,(k∈Z),此时,y取最小值.
,(k∈Z),此时,y取最小值.综上,可得y取最大值时,相应的x的值为x=
 kπ+
kπ+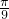 (k∈Z);y取最小值时,相应的x的值为x=
(k∈Z);y取最小值时,相应的x的值为x= kπ-
kπ- ,k∈Z.
,k∈Z.(2)由 2kπ-
 ≤3x+
≤3x+ ≤2kπ+
≤2kπ+ ,k∈z,可得
,k∈z,可得  kπ-
kπ- ≤x≤
≤x≤ kπ+
kπ+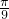 ,
,故函数单调递增区间为[
 kπ-
kπ- ,
, kπ+
kπ+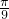 ](k∈Z).
](k∈Z).由 2kπ+
 ≤3x+
≤3x+ ≤2kπ+
≤2kπ+ ,k∈z,可得
,k∈z,可得  kπ+
kπ+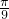 ≤x≤
≤x≤ kπ+
kπ+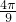 ,
,故函数单调递减区间为[
 kπ+
kπ+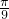 ,
, kπ+
kπ+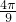 ](k∈Z);
](k∈Z);(3)先将正弦曲线上每一点的横坐标变为原来的
 (纵坐标不变),得到y=
(纵坐标不变),得到y= sin3x 的图象.
sin3x 的图象.再将所得图象向左平移
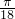 个单位,然后将所得图象上每一点的纵坐标变为原来的
个单位,然后将所得图象上每一点的纵坐标变为原来的 (横坐标不变),
(横坐标不变),得到y=
 sin(3x+
sin(3x+ )的图象.
)的图象.最后将所得图象向上平移一个单位,即可得到y=
 sin(3x+
sin(3x+ )+1的图象.
)+1的图象.分析:(1)由3x+
 =2kπ+
=2kπ+ ,k∈z,和 3x+
,k∈z,和 3x+ =2kπ-
=2kπ- ,k∈z,求得x的值,即为所求.
,k∈z,求得x的值,即为所求. (2)由 2kπ-
 ≤3x+
≤3x+ ≤2kπ+
≤2kπ+ ,k∈z,求得x的范围,即得函数的增区间;由2kπ+
,k∈z,求得x的范围,即得函数的增区间;由2kπ+ ≤3x+
≤3x+ ≤2kπ+
≤2kπ+ ,
,k∈z,求得x的范围,即得函数的减区间.
(3)先将y=sinx上每一点的横坐标变为原来的
 ,再将所得图象向左平移
,再将所得图象向左平移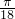 个单位,然后将所得图象上每一点的纵坐标变为原来的
个单位,然后将所得图象上每一点的纵坐标变为原来的 ,再把所得图象向上平移一个单位,即可得到y=
,再把所得图象向上平移一个单位,即可得到y= sin(3x+
sin(3x+ )+1的图象.
)+1的图象.点评:本题主要考查y=Asin(ωx+∅)的图象变换,求三角函数的单调区间和最值的方法,属于中档题.

练习册系列答案
相关题目
已知函数y=|sin(2x-
)|,则以下说法正确的是( )
| π |
| 6 |
A、周期为
| ||||
B、函数图象的一条对称轴是直线x=
| ||||
C、函数在[
| ||||
| D、函数是偶函数 |

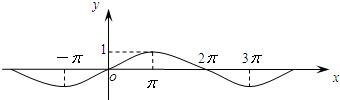 已知函数y=sinωx(ω>0)的图象如图所示,把y=sinωx的图象所有点向右平移
已知函数y=sinωx(ω>0)的图象如图所示,把y=sinωx的图象所有点向右平移