题目内容
3.已知△ABC的内角∠A、∠B、∠C所对的边分别为a、b、c,且∠A=$\frac{π}{3}$,若a=1,则△ABC的周长l的取值范围是( )| A. | (1,2) | B. | (1,3] | C. | (2,3] | D. | (1,3) |
分析 利用正弦定理表示出b,c,得到三角形的周长,然后通过两角和以及角的范围求解即可.
解答 解:△ABC的内角∠A、∠B、∠C所对的边分别为a、b、c,且∠A=$\frac{π}{3}$,若a=1,
可得b=$\frac{sinB}{sin\frac{π}{3}}$,c=$\frac{sinC}{sin\frac{π}{3}}$,A+B+C=π,B=$\frac{2π}{3}-C$
l=a+b+c=1+$\frac{sinB}{sin\frac{π}{3}}+\frac{sinC}{sin\frac{π}{3}}$=1+$\frac{2\sqrt{3}}{3}$(sinB+sinC)
=1+$\frac{2\sqrt{3}}{3}$(sinC+sin($\frac{2π}{3}-C$))
=1+$\frac{2\sqrt{3}}{3}$(sinC+$\frac{\sqrt{3}}{2}$cosC+$\frac{1}{2}$sinC)
=1+$\frac{2\sqrt{3}}{3}$($\frac{3}{2}$sinC+$\frac{\sqrt{3}}{2}$cosC)
=1+2($\frac{\sqrt{3}}{2}$sinC+$\frac{1}{2}$cosC)
=1+2sin(C+$\frac{π}{6}$),∵$\frac{π}{6}$<C+$\frac{π}{6}$<$\frac{5π}{6}$.
∴1+2sin(C+$\frac{π}{6}$)∈(2,3].
故选:C.
点评 本题考查三角形的解法,正弦定理的应用,考查两角和与差的三角函数,是中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
8.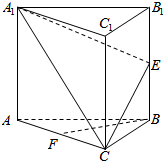 如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
(1)求证:BF∥平面A1EC;
(2)求证:平面A1EC⊥平面ACC1A1.
(3)若各棱长相等,求二面角E-AC-B正切值.
 如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.(1)求证:BF∥平面A1EC;
(2)求证:平面A1EC⊥平面ACC1A1.
(3)若各棱长相等,求二面角E-AC-B正切值.
15.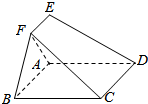 在如图所示的多面体ABCDEF中.四边形ABCD为矩形.EA⊥平面ABCD.EF∥AB,AB=4,AE=EF=2,则点D到平面FBC的距离为( )
在如图所示的多面体ABCDEF中.四边形ABCD为矩形.EA⊥平面ABCD.EF∥AB,AB=4,AE=EF=2,则点D到平面FBC的距离为( )
 在如图所示的多面体ABCDEF中.四边形ABCD为矩形.EA⊥平面ABCD.EF∥AB,AB=4,AE=EF=2,则点D到平面FBC的距离为( )
在如图所示的多面体ABCDEF中.四边形ABCD为矩形.EA⊥平面ABCD.EF∥AB,AB=4,AE=EF=2,则点D到平面FBC的距离为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 4 |
13.已知F1、F2分别是双曲线x2-$\frac{{y}^{2}}{6}$=1的左、右焦点,点P为右支上一点,O为坐标原点,若向量($\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$)与$\overrightarrow{P{F}_{2}}$的夹角为120°,则点F2到直线PF1的距离为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{21}$ |
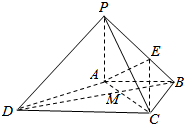 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB∥DC,AB⊥BC,且PA=AB=BC=$\frac{1}{2}$CD,BE=$\frac{1}{3}$BP.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB∥DC,AB⊥BC,且PA=AB=BC=$\frac{1}{2}$CD,BE=$\frac{1}{3}$BP.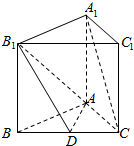 已知正三棱柱ABC-A1B1C1中,BC=1,D是棱BC上的动点.
已知正三棱柱ABC-A1B1C1中,BC=1,D是棱BC上的动点.
 如图,PA⊥平面ABC,∠ACB=90°,AB=$\sqrt{2}$,PA=BC=1,求二面角P-BC-A的大小.
如图,PA⊥平面ABC,∠ACB=90°,AB=$\sqrt{2}$,PA=BC=1,求二面角P-BC-A的大小.