题目内容
9.设不等式-2<|x-1|-|x+2|<0的解集为M,a,b∈M.(Ⅰ)求M;
(Ⅱ)比较|1-4ab|与2|a-b|的大小,并说明理由.
分析 (Ⅰ)化简函数f(x)=|x-1|-|x+2|的解析式,从而求得f(x)<0的解集M.
(Ⅱ)由(Ⅰ)得a2<$\frac{1}{4}$,b2<$\frac{1}{4}$. 化简|1-4ab|2-4|a-b|2=(4a2-1)(4b2-1)>0,可得结论.
解答 解:(Ⅰ)记f(x)=|x-1|-|x+2|=$\left\{\begin{array}{l}3,x≤-2\\-2x-1,-2<x<1\\-3,x≥1\end{array}\right.$,
当-2<x<1时,由-2<-2x-1<0,解得-$\frac{1}{2}$<x<$\frac{1}{2}$,则M=(-$\frac{1}{2}$,$\frac{1}{2}$).
(Ⅱ)由(Ⅰ)得a2<$\frac{1}{4}$,b2<$\frac{1}{4}$.
因为|1-4ab|2-4|a-b|2=(1-8ab+16a2b2)-4(a2-2ab+b2)
=(4a2-1)(4b2-1)>0,
所以|1-4ab|2>4|a-b|2,故|1-4ab|>2|a-b|.
点评 本题主要考查绝对值不等式的解法,分段函数的应用,用比较法证明不等式,属于中档题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
19.已知结合集合A={x|1≤3x<9},B={y|y=sinx,x∈R},则A∩B=( )
| A. | [0,1) | B. | [0,1] | C. | (0,1) | D. | [-1,2) |
17.执行如图所示的程序框图,则输出的T值为( )
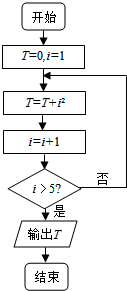

| A. | 30 | B. | 54 | C. | 55 | D. | 91 |