题目内容
已知点A(-3,8)、B(2,2),点P是x轴上的点,求当|AP|+|PB|最小时的点P的坐标.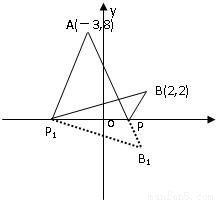
【答案】分析:在x轴上,任取一点P1,作B关于x轴的对称点B1,连接AB1交x轴于P,则|PA|+|PB|≤|P1A|+|P1B|,
点P即为所求,由两点式求出直线AB1的方程,令y=0,可得点P的坐标.
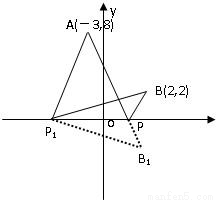
解答:解:(如图)在x轴上,任取一点P1,作B(2,2)关于x轴的对称点B1(2,-2),
连接P1B1,P1A,P1B,连接AB1交x轴于P,
则|P1A|+|P1B|=|P1A|+|P1B1|≥|AB1|,又|PA|+|PB|=|PA|+|PB1|=|AB1|,
∴|PA|+|PB|≤|P1A|+|P1B|,∴点P即为所求,
由两点式求出直线AB1的方程: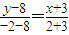 ,即 2x+y-2=0,令y=0,则x=1.∴点P的坐标为(1,0).
,即 2x+y-2=0,令y=0,则x=1.∴点P的坐标为(1,0).
点评:本题考查求一个点关于x轴的对称点的坐标的方法,线段的中垂线的性质,以及用两点式求直线的方程,体现了数形结合的数学思想.
点P即为所求,由两点式求出直线AB1的方程,令y=0,可得点P的坐标.
解答:解:(如图)在x轴上,任取一点P1,作B(2,2)关于x轴的对称点B1(2,-2),
连接P1B1,P1A,P1B,连接AB1交x轴于P,
则|P1A|+|P1B|=|P1A|+|P1B1|≥|AB1|,又|PA|+|PB|=|PA|+|PB1|=|AB1|,
∴|PA|+|PB|≤|P1A|+|P1B|,∴点P即为所求,
由两点式求出直线AB1的方程:
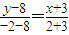 ,即 2x+y-2=0,令y=0,则x=1.∴点P的坐标为(1,0).
,即 2x+y-2=0,令y=0,则x=1.∴点P的坐标为(1,0).
点评:本题考查求一个点关于x轴的对称点的坐标的方法,线段的中垂线的性质,以及用两点式求直线的方程,体现了数形结合的数学思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
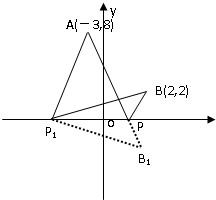 已知点A(-3,8)、B(2,2),点P是x轴上的点,求当|AP|+|PB|最小时的点P的坐标.
已知点A(-3,8)、B(2,2),点P是x轴上的点,求当|AP|+|PB|最小时的点P的坐标.