题目内容
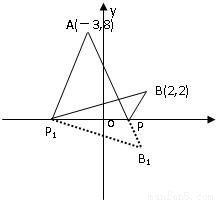
已知点A(-3,8),B(2,2).(1)在x轴上找到一点P,使得|AP|+|PB|取得最小值,求点P的坐标;
(2)在y轴上找一点Q,使得|AQ|-|QB|的绝对值取到最大值,求点Q的坐标.
分析:(1)先求出点A关于x轴的对称点A′的坐标,再用点斜式求出直线A′B的方程,求出直线与x轴的交点即可;
(2)先求出点A关于y轴的对称点A′的坐标,再用点斜式求出直线A′B的方程,求出直线与y轴的交点即可
(2)先求出点A关于y轴的对称点A′的坐标,再用点斜式求出直线A′B的方程,求出直线与y轴的交点即可
解答:解:(1)∵点A(-3,8),
∴点A关于x轴的对称点A′的坐标为(-3,-8),
∵B(2,2),
∴直线A′B的方程为y-2=2(x-2),即y=2x-6
当y=0时,x=3.
∴P(3,0);
(2)∵点A(-3,8),
∴点A关于y轴的对称点A′的坐标为(3,8),
∵B(2,2),
∴直线A′B的方程为y-2=6(x-2),即y=6x-10,
当x=0时,y=-10.
∴Q(0,-10).
∴点A关于x轴的对称点A′的坐标为(-3,-8),
∵B(2,2),
∴直线A′B的方程为y-2=2(x-2),即y=2x-6
当y=0时,x=3.
∴P(3,0);
(2)∵点A(-3,8),
∴点A关于y轴的对称点A′的坐标为(3,8),
∵B(2,2),
∴直线A′B的方程为y-2=6(x-2),即y=6x-10,
当x=0时,y=-10.
∴Q(0,-10).
点评:本题考查的是轴对称-最短路线问题,熟知“两点之间线段最短”是解答此题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
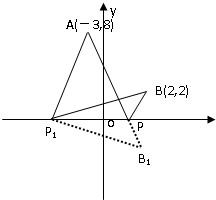 已知点A(-3,8)、B(2,2),点P是x轴上的点,求当|AP|+|PB|最小时的点P的坐标.
已知点A(-3,8)、B(2,2),点P是x轴上的点,求当|AP|+|PB|最小时的点P的坐标.