题目内容
设双曲线4x2－y2=1的两条渐近线与直线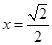
围成的三角形区域（包括边界）为E， P（x, y）为该区域内的一动点，则目标函数z=x－2y的最小值为________.
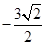
解析试题分析：双曲线4x2－y2=1的渐近线为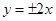
，画出可行域，再画出目标函数，通过平移可知在
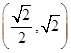处取到最小值，最小值为.
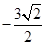考点：本小题主要考查双曲线的渐近线的计算和线性规划问题的求解，考查学生画图、用图的能力.
点评：解决线性规划问题的关键是正确画出可行域和目标函数，确定取得最值点的点.
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
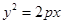的焦点与双曲线
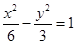的右焦点重合，则
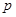的值 ．
中，
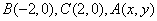，给出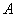
的轨迹方程，下表给出了一些条件及方程：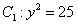
、
、
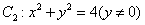
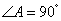
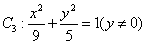
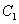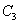填入）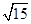 
，0)，则椭圆的标准方程是 
被直线l：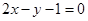
截得的弦长为 
在曲线
上，点
在曲线
上，则
的最小值等于 ．
的左、右焦点，点P是双曲线上的点，且|P F1|=3，则|PF2|的值为 .
中，双曲线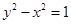
的离心率为 .
中，椭圆
的中心为原点，焦点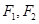
在
轴上，离心率为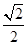
。过F1的直线交椭圆C于
两点，且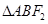
的周长为16，那么