题目内容
【题目】已知四面体![]() 的棱长满足
的棱长满足![]() ,
,![]() ,现将四面体
,现将四面体![]() 放入一个主视图为等边三角形的圆锥中,使得四面体
放入一个主视图为等边三角形的圆锥中,使得四面体![]() 可以在圆锥中任意转动,则圆锥侧面积的最小值为___________.
可以在圆锥中任意转动,则圆锥侧面积的最小值为___________.
【答案】![]()
【解析】
若满足题意,则四面体的外接球应该内切于圆锥即可.先求得四面体外接球的半径,再根据该球内切于圆锥,即可求得圆锥侧面积的最小值.
若满足题意,则四面体的外接球应该内切于圆锥即可.
为逻辑清晰,我们将问题主要分为两步.
第一步:求得四面体![]() 外接球半径.
外接球半径.
记![]() 外心为
外心为![]() ,过
,过![]() 作平面
作平面![]() 的垂线
的垂线![]() ,
,
记外接球球心为![]() ,连接
,连接![]() .
.
则外接球半径![]() .下面求解
.下面求解![]() .
.

在![]() 中,由余弦定理可得
中,由余弦定理可得![]() ,
,
则由同角三角函数关系可得![]() .
.
故![]() 外接圆半径
外接圆半径![]() .
.
将![]() 的图形单独抽取出来,取
的图形单独抽取出来,取![]() 中点为
中点为![]() .如上面由图所示:
.如上面由图所示:
容易知: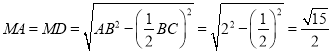 .
.
在![]() 中,因为
中,因为![]() ,
,![]() ,
,
故可得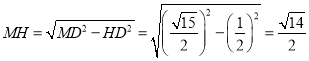 ,
,
![]() .
.
故可得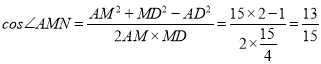 .
.
又因为![]() ,
,
解得![]() .
.
在![]() 中,容易得
中,容易得![]() .
.
故可得![]() .
.
在![]() 中,
中,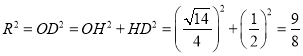 .
.
故可得四面体![]() 外接球半径
外接球半径![]() .
.
第二步:根据外接球半径和圆锥的关系,求得圆锥的母线和底面圆半径.
若满足题意,则该外接球应该内切于圆锥,
作出轴截面的平面图,其中![]() 点为
点为![]() 的中点,如下所示:
的中点,如下所示:

该截面图中![]() .
.
由题可知![]() 为等边三角形,故可得
为等边三角形,故可得![]() ;
;
在![]() 中,
中,![]() ,解得
,解得![]() .
.
故可得圆锥的底面圆半径为![]() .母线长
.母线长![]() .
.
故可得圆锥的侧面积为![]()
![]() .
.
故答案为:![]() .
.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案【题目】随着互联网金融的不断发展,很多互联网公司推出余额增值服务产品和活期资金管理服务产品,如蚂蚁金服旗下的“余额宝”,腾讯旗下的“财富通”,京东旗下“京东小金库”.为了调查广大市民理财产品的选择情况,随机抽取1200名使用理财产品的市民,按照使用理财产品的情况统计得到如下频数分布表:
分组 | 频数(单位:名) |
使用“余额宝” |
|
使用“财富通” |
|
使用“京东小金库” | 30 |
使用其他理财产品 | 50 |
合计 | 1200 |
已知这1200名市民中,使用“余额宝”的人比使用“财富通”的人多160名.
(1)求频数分布表中![]() ,
,![]() 的值;
的值;
(2)已知2018年“余额宝”的平均年化收益率为![]() ,“财富通”的平均年化收益率为
,“财富通”的平均年化收益率为![]() .若在1200名使用理财产品的市民中,从使用“余额宝”和使用“财富通”的市民中按分组用分层抽样方法共抽取7人,然后从这7人中随机选取2人,假设这2人中每个人理财的资金有10000元,这2名市民2018年理财的利息总和为
.若在1200名使用理财产品的市民中,从使用“余额宝”和使用“财富通”的市民中按分组用分层抽样方法共抽取7人,然后从这7人中随机选取2人,假设这2人中每个人理财的资金有10000元,这2名市民2018年理财的利息总和为![]() ,求
,求![]() 的分布列及数学期望.注:平均年化收益率,也就是我们所熟知的利息,理财产品“平均年化收益率为
的分布列及数学期望.注:平均年化收益率,也就是我们所熟知的利息,理财产品“平均年化收益率为![]() ”即将100元钱存入某理财产品,一年可以获得3元利息.
”即将100元钱存入某理财产品,一年可以获得3元利息.
【题目】某商场为改进服务质量,在进场购物的顾客中随机抽取了![]() 人进行问卷调查.调查后,就顾客“购物体验”的满意度统计如下:
人进行问卷调查.调查后,就顾客“购物体验”的满意度统计如下:
满意 | 不满意 | |
男 |
|
|
女 |
|
|
![]() 是否有
是否有![]() 的把握认为顾客购物体验的满意度与性别有关?
的把握认为顾客购物体验的满意度与性别有关?
![]() 若在购物体验满意的问卷顾客中按照性别分层抽取了
若在购物体验满意的问卷顾客中按照性别分层抽取了![]() 人发放价值
人发放价值![]() 元的购物券.若在获得了
元的购物券.若在获得了![]() 元购物券的
元购物券的![]() 人中随机抽取
人中随机抽取![]() 人赠其纪念品,求获得纪念品的
人赠其纪念品,求获得纪念品的![]() 人中仅有
人中仅有![]() 人是女顾客的概率.
人是女顾客的概率.
附表及公式: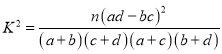 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
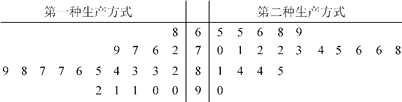
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]() ,
,
|
|
|
|
|
|
|
|