题目内容
如图所示,已知C点在圆O直径BE的延长线上,CA切圆O于A点,∠ACB的平分线CD交AE于点F,交AB于点D.
(1)求∠ADF的度数;
(2)若AB=AC,求AC∶BC.
(1) 45° (2)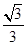
解析解:(1)∵AC为圆O的切线,
∴∠B=∠EAC,
又∵CD是∠ACB的平分线,
∴∠ACD=∠DCB,
∴∠B+∠DCB=∠EAC+∠ACD,即∠ADF=∠AFD.
又∵BE为圆O的直径,∴∠DAE=90°,
∴∠ADF=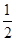 (180°-∠DAE)=45°.
(180°-∠DAE)=45°.
(2)∵∠B=∠EAC,∠ACB=∠ACB,
∴△ACE∽△BCA,
∴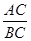 =
=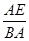 .又∵AB=AC,∴∠B=∠ACB=30°,
.又∵AB=AC,∴∠B=∠ACB=30°,
∴在Rt△ABE中, 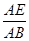 ="tan" B="tan" 30°=
="tan" B="tan" 30°=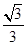 ,
,
∴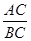 =
=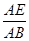 =
=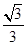 .
.

练习册系列答案
相关题目
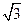 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.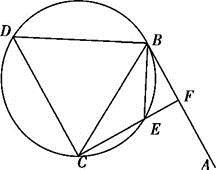
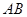 是圆
是圆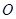 的直径,
的直径, 是
是 是圆
是圆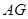 的垂线,交直线
的垂线,交直线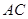 于点
于点 ,交直线
,交直线 于点
于点 ,过点
,过点 .
.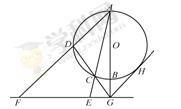
 四点共圆;(2)若
四点共圆;(2)若 ,求
,求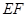 的长.
的长.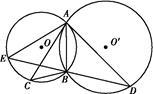
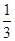 BC,CE=
BC,CE=

 ,连接DE交BC于点F,AC=4,BC=3.求证:
,连接DE交BC于点F,AC=4,BC=3.求证:

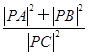 .
.