题目内容
已知点M,N的坐标分别为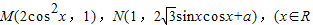 ,a∈R,a是常数),且
,a∈R,a是常数),且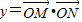 (O为坐标点).
(O为坐标点).(1)求y关于x的函数关系式y=f(x),并求出f(x)的最小正周期;
(2)若
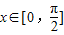 时,f(x)的最大值为4,求a的值,并说明此时f(x)的图象可由
时,f(x)的最大值为4,求a的值,并说明此时f(x)的图象可由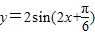 的图象经过怎样的变换而得到.
的图象经过怎样的变换而得到.
【答案】分析:(1)由已知中M,N的坐标分别为 ,a∈R,a是常数),可得
,a∈R,a是常数),可得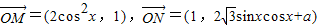 ,进而由向量数量积公式,求出函数关系式y=f(x),化为正弦型函数的形式后,即可求出f(x)的最小正周期;
,进而由向量数量积公式,求出函数关系式y=f(x),化为正弦型函数的形式后,即可求出f(x)的最小正周期;
(2)根据正弦型函数的性质,根据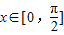 时,f(x)的最大值为4,我们可以求出a值,进而根据函数图象的平移变换法则,得到平移方法.
时,f(x)的最大值为4,我们可以求出a值,进而根据函数图象的平移变换法则,得到平移方法.
解答:解:(1)∵M,N的坐标分别为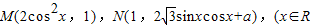 ,a∈R,a是常数),
,a∈R,a是常数),
∴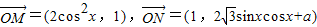
又∵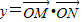
∴y=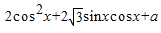 =1+2cos2x+
=1+2cos2x+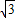 sin2x+a=2sin(2x+
sin2x+a=2sin(2x+ )+a+1(6分)
)+a+1(6分)
∵ω=2
∴f(x)的最小正周期T=π
(2)当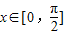 时,2x+
时,2x+ ∈[
∈[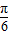 ,
, ]
]
∴当2x+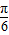 =
= 即x=
即x=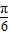 时,y取最大值,此时2+a+1=4
时,y取最大值,此时2+a+1=4
∴a+1
此时y=2sin(2x+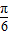 )+2
)+2
∴只需将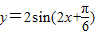 的图象向上平移2个单位便可得y=f(x)的图象(7分)
的图象向上平移2个单位便可得y=f(x)的图象(7分)
点评:本题考查的知识点是平面向量的数量积运算,正弦型函数的图象和性质,函数图象的平移变换法则,其中根据平面向量的数量积公式和辅助角公式,求出函数的解析式是解答本题的关键.
 ,a∈R,a是常数),可得
,a∈R,a是常数),可得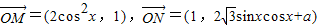 ,进而由向量数量积公式,求出函数关系式y=f(x),化为正弦型函数的形式后,即可求出f(x)的最小正周期;
,进而由向量数量积公式,求出函数关系式y=f(x),化为正弦型函数的形式后,即可求出f(x)的最小正周期;(2)根据正弦型函数的性质,根据
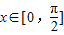 时,f(x)的最大值为4,我们可以求出a值,进而根据函数图象的平移变换法则,得到平移方法.
时,f(x)的最大值为4,我们可以求出a值,进而根据函数图象的平移变换法则,得到平移方法.解答:解:(1)∵M,N的坐标分别为
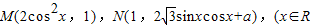 ,a∈R,a是常数),
,a∈R,a是常数),∴
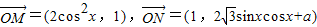
又∵
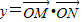
∴y=
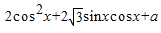 =1+2cos2x+
=1+2cos2x+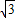 sin2x+a=2sin(2x+
sin2x+a=2sin(2x+ )+a+1(6分)
)+a+1(6分)∵ω=2
∴f(x)的最小正周期T=π
(2)当
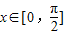 时,2x+
时,2x+ ∈[
∈[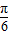 ,
, ]
]∴当2x+
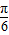 =
= 即x=
即x=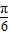 时,y取最大值,此时2+a+1=4
时,y取最大值,此时2+a+1=4∴a+1
此时y=2sin(2x+
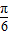 )+2
)+2∴只需将
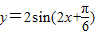 的图象向上平移2个单位便可得y=f(x)的图象(7分)
的图象向上平移2个单位便可得y=f(x)的图象(7分)点评:本题考查的知识点是平面向量的数量积运算,正弦型函数的图象和性质,函数图象的平移变换法则,其中根据平面向量的数量积公式和辅助角公式,求出函数的解析式是解答本题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 的左右焦点为
的左右焦点为 ,抛物线C:
,抛物线C: 以F2为焦点且与椭圆相交于点M
以F2为焦点且与椭圆相交于点M 、N
、N ,直线
,直线 与抛物线C相切
与抛物线C相切 ,
, .直线
.直线 相交于点M,且它们的斜率之积为-2.
相交于点M,且它们的斜率之积为-2. 的直线
的直线 交动点M的轨迹于C、D两点, 且N为线段CD的中点,求直线
交动点M的轨迹于C、D两点, 且N为线段CD的中点,求直线