题目内容

已知点A、B的坐标分别是，.直线相交于点M，且它们的斜率之积为－2.

(Ⅰ)求动点M的轨迹方程;

(Ⅱ)若过点的直线交动点M的轨迹于C、D两点, 且N为线段CD的中点，求直线的方程.

(1)  (2) 所求直线的方程为


解析:

【解题思路】弦中点问题用“点差法”或联立方程组，利用韦达定理求解

 (Ⅰ)设，

因为,所以化简得:

(Ⅱ) 设 

当直线⊥x轴时,直线的方程为,则,其中点不是N,不合题意

设直线的方程为 

将代入得

…………(1)   …………(2) 

(1)-(2)整理得: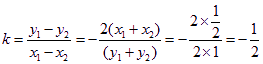 

直线的方程为

即所求直线的方程为

解法二: 当直线⊥x轴时,直线的方程为,则,

其中点不是N,不合题意.

故设直线的方程为,将其代入化简得

由韦达定理得,

又由已知N为线段CD的中点,得,解得,

将代入(1)式中可知满足条件.

此时直线的方程为,即所求直线的方程为

练习册系列答案
相关题目
已知点A，B的坐标分别是（0，-1），（0，1），直线AM，BM相交于点M，且它们的斜率之积-
12
．
（1）求点M轨迹C的方程；
（2）若过点D（2，0）的直线l与（1）中的轨迹C交于不同的两点D、F（E在D、F之间），试求△ODE与△ODF面积之比的取值范围（O为坐标原点）．
【理科生做】已知点A、B的坐标分别是（0，-1），（0，1），直线AM、BM相交于点M，且它们的斜率之积为-1．
（1）求点M轨迹C的方程；
（2）若过点（2，0）且斜率为k的直线l与（1）中的轨迹C交于不同的两点E、F（E在D、F之间），记△ODE与△ODF面积之比为λ，求关于λ和k的关系式，并求出λ取值范围（O为坐标原点）．
已知点A，B的坐标分别是（-1，0），（1，0），直线AM与BM相交于点M，且直线AM的斜率与BM斜率之差是2，求点M的轨迹方程．
已知点A，B的坐标分别是（0，-1），（0，1），直线AM，BM相交于点M，且它们的斜率之积为-
1
2
．
（1）求点M的轨迹C的方程；
（2）过D（2，0）的直线l与轨迹C有两个不同的交点时，求l的斜率的取值范围；
（3）若过D（2，0），且斜率为
14
6
的直线l与（1）中的轨迹C交于不同的E、F（E在D、F之间），求△ODE与△ODF的面积之比．
已知点A、B的坐标分别是A（0，-1），B（0，1），直线AM、BM相交于点M，且它们的斜率之积是2，求点M的轨迹方程，并说明曲线的类型．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网