��Ŀ����
10����������˵���У���ȷ�ĸ����������⡰?x��R������x2-3x-2��0���ķ��ǣ���?x��R��ʹ��x2-3x-2��0��
�ڡ�����p��qΪ�桱�ǡ�����p��qΪ�桱�ı�Ҫ�����������
��?m��R��ʹf��x��=mx${\;}^{{m}^{2}+2m}$���ݺ��������ڣ�0��+�ޣ����ǵ�������
��������x1��x2��x3������xn�ķ���Ϊ1����2x1��2x2��2x3��..2xn�ķ���Ϊ2��������
| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 3�� |
���� ��ȫ������ķ��жϣ�
�����Ӵ�������ٵ��жϣ�
�۶��ݺ��������ϵ��Ϊ1�����ɴ˵ó�m��ֵ��
�ܶ��������X����ΪD��x�������������2X�ķ���Ϊ4D��x����
��� �⣺���ڢ١����⡰?x��R������x2-3x-2��0���ķ��ǣ���?x��R��ʹ��x2-3x-2��0����
�����⡰?x��R������x2-3x-2��0���ķ��ǣ���?x��R��ʹ��x2-3x-2��0������
���ٲ���ȷ��
���ڢڡ�������p��qΪ��ɵõ�������p��qͬʱΪ�棬
������p��qΪ��˵������p��q��������һ��Ϊ�棬
���ɡ�����p��qΪ�桱⇒������p��qΪ�桱��
��������p��qΪ�桱�Ʋ���������p��qΪ�桱��
�ࡰ����p��qΪ�桱�ǡ�����p��qΪ�桱�ı�Ҫ�����������ȷ���ʢ���ȷ��
���ڢ�f��x��=mx${\;}^{{m}^{2}+2m}$���ݺ����Ļ��������ݺ����Ķ��壬�ݺ�������ʽΪy=x����
ϵ��Ϊ1����m=1������y=x3���ڣ�0��+�ޣ���ʱ���������ʢ���ȷ��
���ڢ�������x1��x2��x3������xn�ķ���Ϊ1����$D��x��=\frac{��{x}_{1}-\overline{x}��^{2}+��{x}_{2}-\overline{x}��^{2}+��+��{x}_{n}-\overline{x}��^{2}}{n}$
��2x1��2x2��2x3��..2xn�ķ���ΪΪ$D'��x��=\frac{��2{x}_{1}-2\overline{x}��^{2}+��2{x}_{2}-2\overline{x}��^{2}+��+��2{x}_{n}-2\overline{x}��^{2}}{n}$=4���ʢܲ���ȷ��
��ѡ��C
���� ������Ҫ��������ķ��������١��ݺ����ĸ�����ݷ���ĸ�����ڻ������ͣ�

| A�� | $\frac{{3\sqrt{2}}}{2}$ | B�� | $\sqrt{5}$ | C�� | 5 | D�� | $\frac{9}{2}$ |
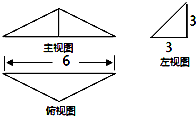
| A�� | 6 | B�� | 9 | C�� | 12 | D�� | 18 |