题目内容
【题目】在平面直角坐标系xOy中,已知椭圆C1: ![]() =1和C2:x2+
=1和C2:x2+ ![]() =1.P为C1上的动点,Q为C2上的动点,w是
=1.P为C1上的动点,Q为C2上的动点,w是 ![]() 的最大值.记Ω={(P,Q)|P在C1上,Q在C2上,且
的最大值.记Ω={(P,Q)|P在C1上,Q在C2上,且 ![]() =w},则Ω中元素个数为( )
=w},则Ω中元素个数为( )
A.2个
B.4个
C.8个
D.无穷个
【答案】D
【解析】解:椭圆C1: ![]() =1和C2:x2+
=1和C2:x2+ ![]() =1.P为C1上的动点,Q为C2上的动点,
=1.P为C1上的动点,Q为C2上的动点,
可设P(6cosα,2sinα),Q(cosβ,3sinβ),0≤α\β<2π,
则 ![]() =6cosαcosβ+6sinαsinβ=6cos(α﹣β),
=6cosαcosβ+6sinαsinβ=6cos(α﹣β),
当α﹣β=2kπ,k∈Z时,w取得最大值6,
则Ω={(P,Q)|P在C1上,Q在C2上,且 ![]() =w}中的元素有无穷多对.
=w}中的元素有无穷多对.
另解:令P(m,n),Q(u,v),则m2+9n2=36,9u2+v2=9,
由柯西不等式(m2+9n2)(9u2+v2)=324≥(3mu+3nv)2,
当且仅当mv=nu,即O、P、Q共线时,取得最大值6,
显然,满足条件的P、Q有无穷多对,D项正确.
故选:D.
设出P(6cosα,2sinα),Q(cosβ,3sinβ),0≤α\β<2π,由向量数量积的坐标表示和两角差的余弦公式和余弦函数的值域,可得最大值及取得的条件,即可判断所求元素的个数.

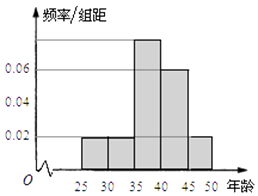
【题目】某单位280名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.
(I)现要从年龄低于40岁的员工中用分层抽样的方法抽取12人,则年龄在第1,2,3组的员工人数分别是多少?
(II)为了交流读书心得,现从上述12人中再随机抽取3人发言,设3人中年龄在[35,40)的人数为ξ,求ξ的数学期望;
(III)为了估计该单位员工的阅读倾向,现对从该单位所有员工中按性别比例抽取的40人做“是否喜欢阅读国学类书籍”进行调查,调查结果如下表所示:(单位:人)
喜欢阅读国学类 | 不喜欢阅读国学类 | 合计 | |
男 | 14 | 4 | 18 |
女 | 8 | 14 | 22 |
合计 | 22 | 18 | 40 |
根据表中数据,我们能否有99%的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系?
附: ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |