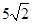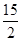题目内容
已知定义域为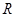 的函数
的函数 满足
满足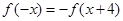 ,则
,则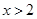 时,
时, 单调递增,若
单调递增,若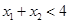 ,且
,且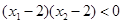 ,则
,则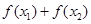 与0的大小关系是( )
与0的大小关系是( )
A.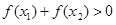 | B.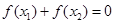 |
C. | D.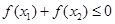 |
C
解析试题分析:因为已知定义域为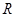 的函数
的函数 满足
满足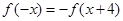 ,则说明函数关于(2,0)成中心对称,同时在x>2,函数递减,则说明x<2,函数也是递减的。由于
,则说明函数关于(2,0)成中心对称,同时在x>2,函数递减,则说明x<2,函数也是递减的。由于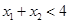 ,则说明数
,则说明数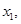 比
比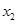 离开中心的距离远,且
离开中心的距离远,且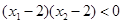 ,则说明
,则说明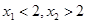 ,那么可知,
,那么可知,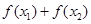 的和会小于零,故选C.
的和会小于零,故选C.
考点:本试题考查了函数的对称性和函数单调性的运用。
点评:解决该试题的关键是对于函数对称性的理解和单调性的运用。通过变量的不等式,来分析两个变量的位置关系,进而结合单调性得到函数值的不等关系,属于中档题。

练习册系列答案
相关题目
设 是定义在R上的函数且
是定义在R上的函数且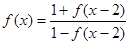 ,且
,且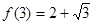 ,则
,则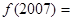
A.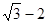 | B.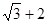 | C. | D.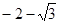 |
函数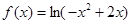 的单调递增区间是( )
的单调递增区间是( )
A.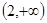 | B.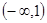 | C.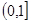 | D.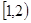 |
已知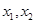 是函数
是函数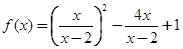 的两个零点,则
的两个零点,则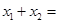
A. | B. | C.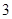 | D. |
下列函数在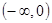 上是增函数的是( )
上是增函数的是( )
A.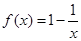 | B.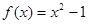 | C. | D.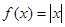 |
已知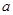 是单调函数
是单调函数 的一个零点,且
的一个零点,且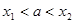 则( )
则( )
A.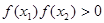 | B.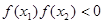 |
C.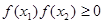 | D.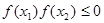 |
已知函数 是定义域为R的偶函数,且
是定义域为R的偶函数,且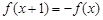 ,若
,若 在
在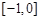 上是增函数,那么
上是增函数,那么 在
在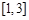 上是
上是
| A.增函数 | B.减函数 | C.先增后减的函数 | D.先减后增的函数 |
定义在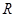 上的函数
上的函数 既是偶函数又是周期函数,若
既是偶函数又是周期函数,若 的最小正周期是
的最小正周期是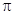 ,且当
,且当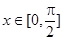 时,
时,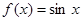 ,则
,则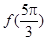 的值为( )
的值为( )
A.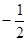 | B.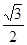 | C. | D.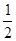 |
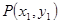 、
、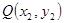 之间的“理想距离”为:
之间的“理想距离”为: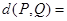
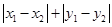 ;若
;若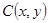 到点
到点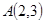 、
、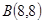 的“理想距离”相等,其中实数
的“理想距离”相等,其中实数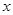 、
、 满足
满足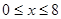 、
、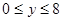 ,则所有满足条件的点
,则所有满足条件的点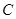 的轨迹的长度之和是
的轨迹的长度之和是