题目内容
1.水平放置的△ABC,若其BC边与x轴平行,BC=a,其直观图△A′B′C′是以B′C′为斜边的等腰直角三角形,则△ABC的面积为$\frac{\sqrt{2}}{2}$a2.分析 由题意,△ABC是直角三角形,AB⊥BC,BC=a,AB=$\sqrt{2}$a,即可求出△ABC的面积.
解答 解:由题意,△ABC是直角三角形,AB⊥BC,BC=a,AB=$\sqrt{2}$a,
∴△ABC的面积为$\frac{1}{2}•a•\sqrt{2}a$=$\frac{\sqrt{2}}{2}$a2.
故答案为:$\frac{\sqrt{2}}{2}$a2.
点评 本题考查了平面图形直观图的画法,解答的关键是熟记斜二测画法的要点和步骤,从而还原得到原图形,求出面积.

练习册系列答案
相关题目
16.函数f(x)=lo${g}_{\frac{1}{2}}$(x2-ax)在区间[2,4]上是减函数,则实数a的取值范围是( )
| A. | 2<a≤4 | B. | a≤4 | C. | a<2 | D. | a≤2 |
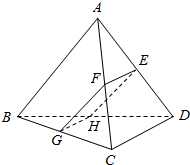 如图,三棱锥A-BCD中,对棱AB与CD所成角为60°,且AB=CD=α,该三棱锥被一平面所截,截面为平行四边形EFGH.
如图,三棱锥A-BCD中,对棱AB与CD所成角为60°,且AB=CD=α,该三棱锥被一平面所截,截面为平行四边形EFGH.