题目内容
已知函数![]() 和
和![]() 的图象关于原点对称,且
的图象关于原点对称,且![]()
(Ⅰ)解不等式:![]()
(Ⅱ)若函数![]() 在区间[
在区间[![]() ]上单调递增,求实数
]上单调递增,求实数![]() 的取值范围。
的取值范围。
解:(Ⅰ)![]() ,
,![]()
化为![]() ,
, ![]() 或
或![]()
解得![]() 或
或![]() ,原不等式的解集为
,原不等式的解集为![]()
(Ⅱ)![]() ,
,
①当![]() 时,
时,![]() 在区间[
在区间[![]() ]上单调递增,从而
]上单调递增,从而![]()
②当![]() 时,对称轴的方程为
时,对称轴的方程为![]() ,依题意得
,依题意得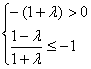 或
或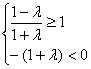 解得
解得![]() 或
或![]()
综合①②得![]()

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
题目内容
已知函数![]() 和
和![]() 的图象关于原点对称,且
的图象关于原点对称,且![]()
(Ⅰ)解不等式:![]()
(Ⅱ)若函数![]() 在区间[
在区间[![]() ]上单调递增,求实数
]上单调递增,求实数![]() 的取值范围。
的取值范围。
解:(Ⅰ)![]() ,
,![]()
化为![]() ,
, ![]() 或
或![]()
解得![]() 或
或![]() ,原不等式的解集为
,原不等式的解集为![]()
(Ⅱ)![]() ,
,
①当![]() 时,
时,![]() 在区间[
在区间[![]() ]上单调递增,从而
]上单调递增,从而![]()
②当![]() 时,对称轴的方程为
时,对称轴的方程为![]() ,依题意得
,依题意得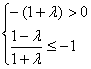 或
或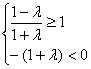 解得
解得![]() 或
或![]()
综合①②得![]()

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案