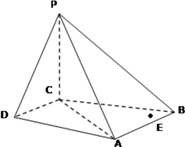题目内容
【题目】如图,直四棱柱ABCD﹣A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD= ![]() ,AA1=3,E为CD上一点,DE=1,EC=3
,AA1=3,E为CD上一点,DE=1,EC=3 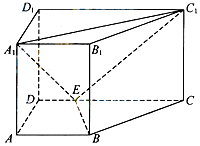
(1)证明:BE⊥平面BB1C1C;
(2)求三棱锥B1﹣EA1C1的体积.
【答案】
(1)证明:过B作CD的垂线交CD于F,
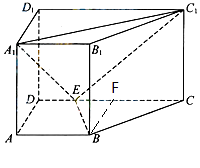
则 ![]()
在 ![]() .
.
在△BCE中,∵BE2+BC2=9=EC2,
∴BE⊥BC,∵BB1⊥平面ABCD,∴BE⊥BB1,
∵BC∩BB1=B,∴BE⊥平面BB1C1C
(2)证明:∵点E到平面A11C1的距离为AA1=3,
∴三棱锥B1﹣EA1C1的体积:
![]() =
= ![]() =
= ![]()
= ![]() =
= ![]() .
.
【解析】(1)过B作CD的垂线交CD于F,推导出BE⊥BC,BE⊥BB1 , 由此能证明BE⊥平面BB1C1C.(2)三棱锥B1﹣EA1C1的体积: ![]() =
= ![]() ,由此能求出结果.
,由此能求出结果.
【考点精析】关于本题考查的直线与平面垂直的判定,需要了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能得出正确答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某种商品价格与该商品日需求量之间的几组对照数据如表:
价格x(元/kg) | 10 | 15 | 20 | 25 | 30 |
日需求量y(kg) | 11 | 10 | 8 | 6 | 5 |
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归方程,当价格x=40元/kg时,日需求量y的预测值为多少?
参考公式:线性回归方程 ![]() ,其中
,其中 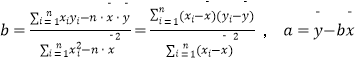 .
.