题目内容
【题目】设 ![]() ,若0≤a≤1,n∈N+且n≥2,求证:f(2x)≥2f(x).
,若0≤a≤1,n∈N+且n≥2,求证:f(2x)≥2f(x).
【答案】证明:∵ ![]() ,
,
∴要证f(2x)≥2f(x),
只要证![]() ,
,
即证![]() (*)
(*)
也即证n[12x+22x+…+(n-1)2x+a·n2x]
≥[1x+2x+…+(n-1)x+a·nx]2 ,
∵0≤a≤1,∴a>a2 , 根据柯西不等式得
n[12x+22x+…+(n-1)2x+a·n2x]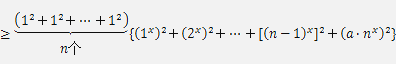 ,
,
≥[1x+2x+…+(n-1)x+a·nx]2 ,
即(*)式显然成立,故原不等式成立.
【解析】本题主要考查了一般形式的柯西不等式,解决问题的关键是将f(2x)>2f(x)具体化,然后再根据式子的结构特点选择合适的证明方法.
【考点精析】本题主要考查了一般形式的柯西不等式的相关知识点,需要掌握一般形式的柯西不等式:![]()
![]() 才能正确解答此题.
才能正确解答此题.

练习册系列答案
相关题目
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对100名六年级学生进行了问卷调查得到如图联表.且平均每天喝500ml以上为常喝,体重超过50kg为肥胖.已知在全部100人中随机抽取1人,抽到肥胖的学生的概率为0.8.
常喝 | 不常喝 | 合计 | |
肥胖 | 60 | ||
不肥胖 | 10 | ||
合计 | 100 |
(1)求肥胖学生的人数并将上面的列联表补充完整;
(2)是否有95%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由. 附:参考公式:x2= ![]()
P(x2≥x0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
x0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |