题目内容
【题目】给定两个长度为1的平面向量 
和 
，它们的夹角为120°．如图所示，点C在以O为圆心的圆弧 
上变动．若 
，其中x，y∈R，试求x+y的最大值． 
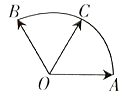
【答案】解：由题意，以O为原点，OA为x轴的正向，建立如图所示的坐标系， 设C（cosθ，sinθ），0≤θ≤ 
，
可得A（1，0），B（﹣ 
， 
）
由 
得，x﹣ y=cosθ， y=sinθ，
∴ 
y= 
sinθ，∴x+y=cosθ+ sinθ=2sin（θ+ 
），
∴x+y的最大值是2．
【解析】建立坐标系，得出点的坐标，进而可得向量的坐标，化已知问题为三角函数的最值求解，可得答案．
【考点精析】本题主要考查了平面向量的基本定理及其意义的相关知识点，需要掌握如果
、
是同一平面内的两个不共线向量，那么对于这一平面内的任意向量
，有且只有一对实数
、
，使
才能正确解答此题．
练习册系列答案
相关题目
【题目】通过随机询问110名性别不同的中学生是否爱好运动，得到如下的列联表：
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由K2= 
得，K2= 
≈7.8
P（K2≥k） | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
参照附表，得到的正确结论是（ ）
A.在犯错误的概率不超过0.1%的前提下，认为“爱好运动与性别有关”
B.有99%以上的把握认为“爱好运动与性别有关”
C.在犯错误的概率不超过0.1%的前提下，认为“爱好运动与性别无关”
D.有99%以上的把握认为“爱好运动与性别无关”
