题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() 分别为椭圆的左、右焦点,点
分别为椭圆的左、右焦点,点![]() 在椭圆上,当
在椭圆上,当![]() 时,
时, ![]() 内切圆的半径为
内切圆的半径为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 相较于
相较于![]() 两点,且
两点,且![]() ,当直线
,当直线![]() 的斜率之和为2时,问:点
的斜率之和为2时,问:点![]() 到直线
到直线![]() 的距离是否存在最大值?若存在,求出最大值;若不存在,说明理由.
的距离是否存在最大值?若存在,求出最大值;若不存在,说明理由.
【答案】(1) 椭圆的方程为![]() ;(2)见解析.
;(2)见解析.
【解析】分析:(1)依据题意,得到![]() ,又由
,又由![]() ,求得
,求得![]() 的值,即可得到椭圆的标准方程;
的值,即可得到椭圆的标准方程;
(2)直线![]() 与椭圆的方程的联立,求得
与椭圆的方程的联立,求得![]() ,由
,由![]() ,代入整理,求得
,代入整理,求得![]() 的值,再由点到直线的距离公式,设
的值,再由点到直线的距离公式,设![]() ,即可求得距离的最大值,得到结论.
,即可求得距离的最大值,得到结论.
详解:
(1)依题意: ![]() ,则
,则![]() ,即
,即![]()
又![]() ,联立解得:
,联立解得: ![]() ,故
,故![]() ,所以椭圆的方程为
,所以椭圆的方程为![]()
(2)设![]() ,
,
联立直线和椭圆的方程得: ![]() ,
,
当![]() 时有:
时有: ![]()
由![]() 得:
得: ![]() ,即
,即![]() ,
,
整理得: ![]() ,所以
,所以![]() ,
,
化简整理得: ![]() ,代入
,代入![]() 得:
得: ![]() ,
,
解之得: ![]() 或
或![]() ,
,
点![]() 到直线
到直线![]() 的距离
的距离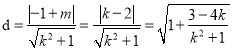 ,
,
设![]() ,易得
,易得![]() 或
或![]() ,则
,则![]() ,
,
当![]() 时
时![]() ;当
;当![]() 时,
时, 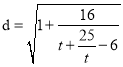 ,
,
若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() ,当
,当![]() 时,
时, 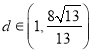
综上所述: 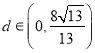 ,故点
,故点![]() 到直线
到直线![]() 的距离没有最大值.
的距离没有最大值.

 阅读快车系列答案
阅读快车系列答案【题目】某测试团队为了研究“饮酒”对“驾车安全”的影响,随机选取![]() 名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.试验数据分别列于表
名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.试验数据分别列于表![]() 和表
和表![]() .统计方法中,同一组数据常用该组区间的中点值作为代表.
.统计方法中,同一组数据常用该组区间的中点值作为代表.
停车距离 |
|
|
|
|
|
频数 |
|
|
|
|
|
表![]()
平均每毫升血液酒精含量 |
|
|
|
|
|
平均停车距离 |
|
|
|
|
|
表![]()
(1)根据最小二乘法,由表![]() 的数据计算
的数据计算![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(2)该测试团队认为:驾驶员酒后驾车的平均“停车距离”![]() 大于无酒状态下(表
大于无酒状态下(表![]() )的停车距离平均数的
)的停车距离平均数的![]() 倍,则认定驾驶员是“醉驾”.请根据(1)中的回归方,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
倍,则认定驾驶员是“醉驾”.请根据(1)中的回归方,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
附:回归方程![]() 中,
中, ,
,![]() .
.
【题目】某测试团队为了研究“饮酒”对“驾车安全”的影响,随机选取![]() 名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.试验数据分别列于表
名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.试验数据分别列于表![]() 和表
和表![]() .统计方法中,同一组数据常用该组区间的中点值作为代表.
.统计方法中,同一组数据常用该组区间的中点值作为代表.
停车距离 |
|
|
|
|
|
频数 |
|
|
|
|
|
表![]()
平均每毫升血液酒精含量 |
|
|
|
|
|
平均停车距离 |
|
|
|
|
|
表![]()
(1)根据最小二乘法,由表![]() 的数据计算
的数据计算![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(2)该测试团队认为:驾驶员酒后驾车的平均“停车距离”![]() 大于无酒状态下(表
大于无酒状态下(表![]() )的停车距离平均数的
)的停车距离平均数的![]() 倍,则认定驾驶员是“醉驾”.请根据(1)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
倍,则认定驾驶员是“醉驾”.请根据(1)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
附:回归方程![]() 中,
中, ,
,![]() .
.