题目内容
已知二次函数 的导函数的图像与直线
的导函数的图像与直线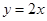 平行,且
平行,且 在
在 处取得极小值
处取得极小值 .设
.设 .
.
(1)若曲线 上的点
上的点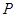 到点
到点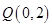 的距离的最小值为
的距离的最小值为 ,求
,求 的值;
的值;
(2)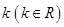 如何取值时,函数
如何取值时,函数 存在零点,并求出零点.
存在零点,并求出零点.
(1) 或
或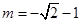 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)先设点 的坐标,利用两点间的距离公式将
的坐标,利用两点间的距离公式将 表示为
表示为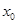 为自变量的函数,利用基本不等式求出相应的最小值,然后列方程求出
为自变量的函数,利用基本不等式求出相应的最小值,然后列方程求出 的值;(2)令
的值;(2)令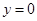 ,将函数
,将函数 的零点转化为求方程
的零点转化为求方程 的根,对首项系数
的根,对首项系数 的符号进行分类讨论,以及在首项系数不为零时对
的符号进行分类讨论,以及在首项系数不为零时对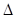 的符号进行分类讨论,从而确定函数在定义域上是否存在零点,并且在零点存在的前提下利用求根公式求出相应的零点值.
的符号进行分类讨论,从而确定函数在定义域上是否存在零点,并且在零点存在的前提下利用求根公式求出相应的零点值.
试题解析:(1)依题可设 (
(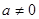 ),则
),则 ;
;
又 的图像与直线
的图像与直线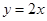 平行
平行 
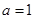
 ,
,  ,
,
设 ,则
,则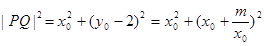

当且仅当 时,
时, 取得最小值,即
取得最小值,即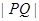 取得最小值
取得最小值
当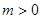 时,
时,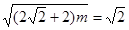 解得
解得
当 时,
时,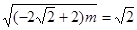 解得
解得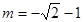
(2)由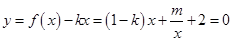 (
(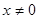 ),得
),得

当 时,方程
时,方程 有一解
有一解 ,函数
,函数 有一零点
有一零点 ;
;
当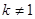 时,方程
时,方程 有二解
有二解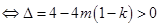 ,
,
若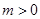 ,
, ,
,
函数 有两个零点
有两个零点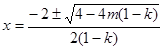 ,即
,即 ;
;
若 ,
, ,
,
函数 有两个零点
有两个零点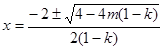 ,即
,即 ;
;
当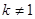 时,方程
时,方程 有一解
有一解 ,
,  ,
,
函数 有一零点
有一零点
综上,当 时, 函数
时, 函数 有一零点
有一零点 ;
;
当 (
(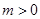 ),或
),或 (
( )时,
)时,
函数 有两个零点
有两个零点 ;
;
当 时,函数
时,函数 有一零点
有一零点 .
.
考点:1.两点间的距离公式;2.基本不等式;3.分类讨论;4.一元二次方程的求解

练习册系列答案
相关题目
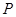 的关系允许近似的满足:
的关系允许近似的满足: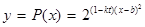 (其中
(其中 为关税的税率,且
为关税的税率,且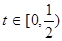 ,
, 为市场价格,
为市场价格,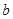 、
、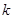 为正常数),当
为正常数),当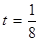 时的市场供应量曲线如图:
时的市场供应量曲线如图: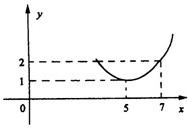
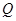 ,它近似满足
,它近似满足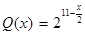 .当
.当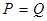 时的市场价格称为市场平衡价格.为使市场平衡价格控制在不低于9元,求税率
时的市场价格称为市场平衡价格.为使市场平衡价格控制在不低于9元,求税率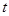 小时内供水总量为
小时内供水总量为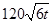 吨(
吨(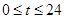 ),从供水开始到第几小时时,蓄水池中的存水量最少?最少水量是多少吨?
),从供水开始到第几小时时,蓄水池中的存水量最少?最少水量是多少吨? ,两个函数
,两个函数 ,
, 的图像关于直线
的图像关于直线 对称.
对称. 满足的关系式;
满足的关系式; 取何值时,函数
取何值时,函数 有且只有一个零点;
有且只有一个零点; 时,在
时,在 上解不等式
上解不等式 .
.
 的极值点,求实数a的值;
的极值点,求实数a的值; 在
在 上为增函数,求实数a的取值范围.
上为增函数,求实数a的取值范围.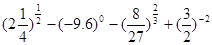 ;⑵
;⑵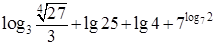 .
.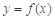 满足:当
满足:当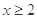 时,
时,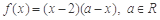 ,当
,当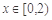 时,
时,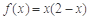 .
.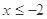 时,
时,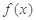 的表达式;
的表达式;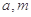 满足什么条件时,函数
满足什么条件时,函数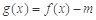 有4个零点,且这4个零点从小到大依次构成等差数列.
有4个零点,且这4个零点从小到大依次构成等差数列.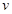 (单位:
(单位: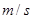 )和燃料的质量
)和燃料的质量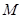 (单位:
(单位: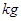 ),火箭(除燃料外)的质量
),火箭(除燃料外)的质量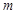 (单位:
(单位: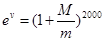 .(
.(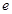 为自然对数的底)
为自然对数的底)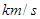 .(结果精确到个位,数据:
.(结果精确到个位,数据: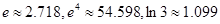 )
)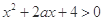 ,对一切
,对一切 恒成立;命题q:函
恒成立;命题q:函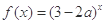 是增函数.若p或q为真,p且q为假,求实数a的取值范围.
是增函数.若p或q为真,p且q为假,求实数a的取值范围.