题目内容
命题p:关于x的不等式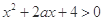 ,对一切
,对一切 恒成立;命题q:函
恒成立;命题q:函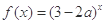 是增函数.若p或q为真,p且q为假,求实数a的取值范围.
是增函数.若p或q为真,p且q为假,求实数a的取值范围.

解析试题分析:先根据不等式恒成立问题以及二次函数的图像与性质求出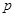 为真时的
为真时的 的取值范围,再根据指数函数的图像与性质求出
的取值范围,再根据指数函数的图像与性质求出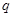 为真时的
为真时的 的取值范围.根据已知条件“
的取值范围.根据已知条件“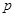 或
或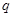 为真,
为真,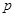 且
且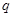 为假”可知,
为假”可知,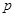 ,
,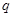 一真一假,那么分别求出“
一真一假,那么分别求出“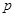 真
真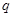 假”和“
假”和“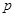 假
假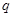 真”情况下的
真”情况下的 的取值范围,两种情况下的
的取值范围,两种情况下的 的取值范围取并集即可.
的取值范围取并集即可.
试题解析: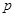 为真:
为真: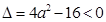 ,解得
,解得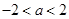 ; 2分
; 2分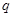 为真:
为真: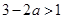 ,解得
,解得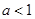 . 4分
. 4分
∵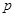 或
或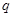 为真,
为真,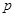 且
且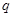 为假,∴
为假,∴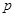 ,
,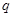 一真一假. 6分
一真一假. 6分
当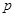 真
真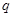 假时,
假时,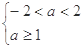
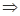
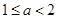 ; 8分
; 8分
当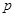 假
假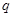 真时,
真时,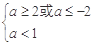
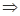
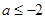 . 10分
. 10分
∴ 的取值范围为
的取值范围为 . 12分
. 12分
考点:1.命题的真假判断及应用;2.不等式恒成立问题;3.二次函数的图像与性质;4.指数函数的图像与性质;5.解不等式

练习册系列答案
相关题目
 的导函数的图像与直线
的导函数的图像与直线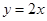 平行,且
平行,且 处取得极小值
处取得极小值 .设
.设 .
. 上的点
上的点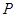 到点
到点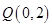 的距离的最小值为
的距离的最小值为 ,求
,求 的值;
的值;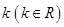 如何取值时,函数
如何取值时,函数 存在零点,并求出零点.
存在零点,并求出零点.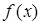 对任意a,b
对任意a,b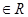 都有
都有 当
当 时,
时, .
.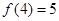 ,解不等式
,解不等式 .
. 个单位的药剂,它在水中释放的浓度
个单位的药剂,它在水中释放的浓度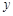 (克/升)随着时间
(克/升)随着时间 (天)变化的函数关系式近似为
(天)变化的函数关系式近似为 ,其中
,其中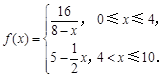 若多次投放,则某一时刻水中的药剂浓度为各次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.
若多次投放,则某一时刻水中的药剂浓度为各次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用. 个单位的药剂,要使接下来的4天中能够持续有效治污,试求
个单位的药剂,要使接下来的4天中能够持续有效治污,试求 ,
, ,且
,且 的解集为
的解集为 .
. 的值;
的值; ,且
,且 ,求证:
,求证:
 ,试利用基本初等函数的图象,判断f(x)有几个零点,并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1).
,试利用基本初等函数的图象,判断f(x)有几个零点,并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1). 上的单调函数
上的单调函数 满足
满足 ,且对任意
,且对任意 都有
都有
 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. .
. 时,求函数
时,求函数 的定义域;
的定义域; 的不等式
的不等式 的解集是
的解集是 ,求
,求 的取值范围.
的取值范围.