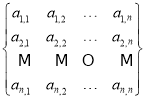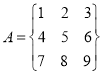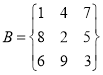题目内容
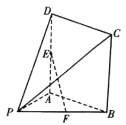
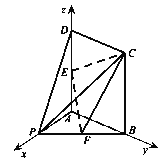
【题目】在如图所示的几何体中,四边形![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() 分别是线段
分别是线段![]() ,
, ![]() 的中点,
的中点, ![]() .
.
![]() 求证:
求证: ![]() 平面
平面![]() ;
;
![]() 求平面
求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)见解析(2)![]()
【解析】(1)取![]() 中点
中点![]() ,连接
,连接![]() ,易得四边形
,易得四边形![]() 为平行四边形,从而
为平行四边形,从而![]()
所以![]() ∥平面
∥平面![]() ;(2)
;(2)![]() 平面
平面![]() ,且四边形
,且四边形![]() 是正方形,
是正方形, ![]() 两两垂直,以
两两垂直,以![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,求出平面
,求出平面![]() 与平面
与平面![]() 的法向量,代入公式得到所成锐二面角的余弦值.
的法向量,代入公式得到所成锐二面角的余弦值.
解: ![]() 方法一:
方法一:
取![]() 中点
中点![]() ,连接
,连接![]() ,
,
![]() 分别是
分别是![]() 中点,
中点, ![]() ,
,
![]() 为
为![]() 中点,
中点, ![]() 为正方形,
为正方形, ![]() ,
,
![]() ,
,![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.

方法二:
取![]() 中点
中点![]() ,连接
,连接![]() ,
, ![]() .
.
![]() 是
是![]() 中点,
中点, ![]() 是
是![]() 中点,
中点, ![]() ,
,
又![]() 是
是![]() 中点,
中点, ![]() 是
是![]() 中点,
中点, ![]() ,
,
![]() ,
, ![]() ,
,
又![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() .
.
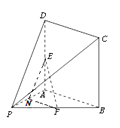
方法三:
取![]() 中点
中点![]() ,连接
,连接![]() ,
, ![]() ,
,
在正方形![]() 中,
中, ![]() 是
是![]() 中点,
中点, ![]() 是
是![]() 中点
中点
![]()
又![]() 是
是![]() 中点,
中点, ![]() 是
是![]() 中点,
中点, ![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() 平面
平面![]() //平面
//平面![]() .
.
![]() 平面
平面![]()
![]() 平面
平面![]() .
.
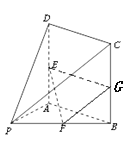
方法四:
![]() 平面
平面![]() ,且四边形
,且四边形![]() 是正方形,
是正方形, ![]() 两两垂直,以
两两垂直,以![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,
,
则![]()
![]()
![]()
![]() ,
,
则设平面![]() 法向量为
法向量为![]() ,
, ![]()
则![]() , 即
, 即![]() , 取
, 取![]() ,
,
![]() ,
,
所以![]()
![]() ,又
,又![]() 平面
平面![]() ,
, ![]() ∥平面
∥平面![]() .
.
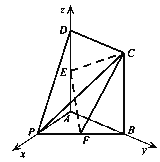
![]()
![]() 平面
平面![]() ,且四边形
,且四边形![]() 是正方形,
是正方形, ![]() 两两垂直,以
两两垂直,以![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,
,
则![]()
![]()
![]()
设平面![]() 法向量为
法向量为![]() ,
,
![]() ,
,
则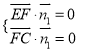 , 即
, 即 ,
,
取![]() ,
,
则设平面![]() 法向量为
法向量为![]() ,
, ![]()
则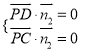 , 即
, 即![]() , 取
, 取![]() ,
,
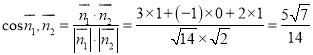 .
.
![]() 平面
平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.
(若第一问用方法四,则第二问部分步骤可省略)

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】下表为北京市居民用水阶梯水价表(单位:元/立方米).
阶梯 | 户年用水量 (立方米) | 水价 | 其中 | ||
自来水费 | 水资源费 | 污水处理费 | |||
第一阶梯 | 0-180(含) | 5.00 | 2.07 | 1.57 | 1.36 |
第二阶梯 | 181-260(含) | 7.00 | 4.07 | ||
第三阶梯 | 260以上 | 9.00 | 6.07 | ||
(Ⅰ)试写出水费![]() (元)与用水量
(元)与用水量![]() (立方米)之间的函数关系式;
(立方米)之间的函数关系式;
(Ⅱ)若某户居民年交水费1040元,求其中自来水费、水资源费及污水处理费各是多少?