题目内容
3．
如图，△ABC是边长为2的正三角形，AE⊥平面ABC，且AE=1，又平面BCD⊥平面ABC，且BD=CD，BD⊥CD．（1）求证：AE∥平面BCD；
（2）求证：平面BDE⊥平面CDE．
分析 （1）取BC的中点M，连接DM、AM，证明AE∥DM，通过直线与平面平行的判定定理证明AE∥平面BCD．
（2）证明DE∥AM，DE⊥CD．利用直线与平面垂直的判定定理证明CD⊥平面BDE．然后证明平面BDE⊥平面CDE．
解答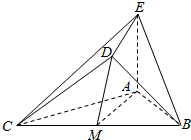 
证明：（1）取BC的中点M，连接DM、AM，
因为BD=CD，且BD⊥CD，BC=2，…（2分）
所以DM=1，DM⊥BC，AM⊥BC，…（3分）
又因为平面BCD⊥平面ABC，
所以DM⊥平面ABC，所以AE∥DM，…（6分）
又因为AE?平面BCD，DM?平面BCD，…（7分）
所以AE∥平面BCD．…（8分）
（2）由（1）已证AE∥DM，又AE=1，DM=1，
所以四边形DMAE是平行四边形，所以DE∥AM．…（10分）
由（1）已证AM⊥BC，又因为平面BCD⊥平面ABC，
所以AM⊥平面BCD，所以DE⊥平面BCD．
又CD?平面BCD，所以DE⊥CD．…（12分）
因为BD⊥CD，BD∩DE=D，所以CD⊥平面BDE．
因为CD?平面CDE，所以平面BDE⊥平面CDE．…（14分）
点评 本题考查平面与平面垂直的判定定理的应用，直线与平面平行与垂直的判定定理的应用，考查空间想象能力逻辑推理能力．
练习册系列答案
相关题目
13．过点M（-1，1）作斜率为$\frac{1}{2}$的直线与椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）相交于A，B两点，若M是线段AB的中点，则椭圆C的离心率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{3}}}{3}$ |
11．不等式$\frac{x-3}{x+2}$≤0的解集为（ ）
| A． | {x|-2＜x≤3} | B． | {x|-2≤x≤3} | C． | {x|x＜-2或x＞3} | D． | {x|-2＜x＜3} |
18．函数y=f（x）的图象如图所示，则以下描述正确的是（ ）
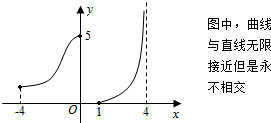
| A． | 函数f（x）的定义域为[-4，4） | |
| B． | 函数f（x）的值域为[0，5] | |
| C． | 此函数在定义域内既不是增函数也不是减函数 | |
| D． | 对于任意的y∈[0，+∞），都有唯一的自变量x与之对应 |
8．若函数f（x）=sin ax+$\sqrt{3}$cos ax（a＞0）的最小正周期为2，则函数f（x）的一个零点为（ ）
| A． | -$\frac{π}{3}$ | B． | $\frac{2}{3}$ | C． | （$\frac{2}{3}$，0） | D． | （0，0） |
12．m，n为实数，命题p：m+n＞2；命题q：m＞1且n＞1，则p是q的（ ）
| A． | 充分不必要的条件 | B． | 必要不充分的条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要的条件 |