题目内容
(2013•和平区二模)已知直线l的参数方程为
(t为参数),圆C的极坐标方程为ρ=2cosθ,若直线l与圆C有唯一公共点,则m的值为
或-3
或-3.
|
| 1 |
| 3 |
| 1 |
| 3 |
分析:将直线l先化为一般方程坐标,将圆C的极坐标方程化成直角坐标方程,然后再计算圆心C到直线l的距离,由圆心到直线的距离等于半径求出实数m.
解答:解:直线l的普通方程为4x-3y+3m=0,圆C的直角坐标方程为x2+y2-2x=0.
所以圆心C(1,0)到直线l的距离d=
=1.
解得m=
或-3.
故答案为:
或-3.
所以圆心C(1,0)到直线l的距离d=
| |4+3m| |
| 5 |
解得m=
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:此题考查参数方程与普通方程的区别和联系,两者要会互相转化,利用直线和圆相切时圆心到直线的距离等于圆的半径求出待定系数的值.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
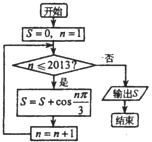 (2013•和平区二模)阅读如图所示的程序框图,运行相应的程序,则输出的结果S的值为( )
(2013•和平区二模)阅读如图所示的程序框图,运行相应的程序,则输出的结果S的值为( ) (2013•和平区二模)已知函数y=Asin(ωx+φ)(A>0,ω>0),|φ|<π)的部分图象如图所示,则它的解析式为( )
(2013•和平区二模)已知函数y=Asin(ωx+φ)(A>0,ω>0),|φ|<π)的部分图象如图所示,则它的解析式为( )