题目内容
5．在集合A={m|关于x的方程x2+mx+$\frac{3}{4}$m+1=0无实根}中随机的取一元素x，恰使lgx有意义的概率为$\frac{4}{5}$．分析 求出集合A，及满足从A中随机的取一元素x，恰使lgx有意义的区间，代入几何概型概率计算公式，可得答案．
解答 解：集合A={m|关于x的方程x2+mx+$\frac{3}{4}$m+1=0无实根}={m|m2-4（$\frac{3}{4}$m+1）＜0}={m|m2-3m-4＜0}=（-1，4），
若使lgx有意义则x∈（0，4），
故从A中随机的取一元素x，恰使lgx有意义的概率P=$\frac{4}{5}$，
故答案为：$\frac{4}{5}$．
点评 本题考查的知识点是几何概型概率计算公式，计算出满足条件和所有基本事件对应的几何量，是解答的关键，难度中档．
练习册系列答案
相关题目
16．
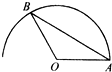如图所示，OA=1，在以O为圆心，OA为半径的半圆弧长任取一点B，则使△AOB的面积大于等于$\frac{1}{4}$的概率为（ ）
如图所示，OA=1，在以O为圆心，OA为半径的半圆弧长任取一点B，则使△AOB的面积大于等于$\frac{1}{4}$的概率为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
20．曲线y=$\frac{{e}^{x}}{{e}^{x}+1}$的切线斜率最大时切线方程是（ ）
| A． | x-4y-2=0 | B． | x+4y+2=0 | C． | x-4y+2=0 | D． | x+4y-2=0 |
10．抛物线y2=x上的点到直线x-2y+3=0的距离的最小值是（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{\sqrt{5}}{5}$ | D． | $\frac{2\sqrt{5}}{5}$ |