题目内容
定义在R上的函数f(x)满足f(x)=f(x+2),当x∈[3,5]时,f(x)=2﹣|x﹣4|,则( )
A.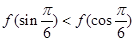 | B. |
C. | D. |
D
解析试题分析:利用函数的周期性及x∈[3,5]时的表达式f(x)=2-|x-4|,可求得x∈[-1,1]时的表达式,从而可判断逐个选项的正误。解:∵f(x+2)=f(x),∴函数f(x)是周期为2的周期函数,又当x∈[3,5]时f(x)=2-|x-4|,∴当-1≤x≤1时,x+4∈[3,5],∴f(x)=f(x+4)=2-|x|,∴f(sin ))=f(
))=f( )=
)= -
-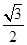 =f(cos
=f(cos  )),排除A, f(sin1)=2-sin1<2-cos1=f(cos1)排除B, f(sin
)),排除A, f(sin1)=2-sin1<2-cos1=f(cos1)排除B, f(sin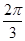 ))=2-
))=2-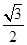 <2-
<2- =f(cos
=f(cos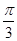 ))=f(cos
))=f(cos 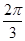 ),D正确; f(sin2)=2-sin2<2-(-cos2)=f(cos2)排除C.故选D
),D正确; f(sin2)=2-sin2<2-(-cos2)=f(cos2)排除C.故选D
考点:函数的周期性
点评:本题考查函数的周期性,难点在于求x∈[-1,1]时的表达式,属于中档题.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
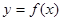 和函数
和函数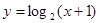 的图像关于直线
的图像关于直线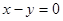 对称,
对称,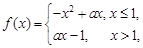 若
若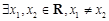 ,使得
,使得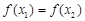 成立,则实数
成立,则实数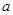 的取值范围是 .
的取值范围是 .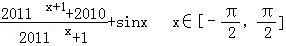 的最大值为M,最小值为N,那么M+N= _________ .
的最大值为M,最小值为N,那么M+N= _________ .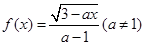 在区间(0,1]上是减函数,则
在区间(0,1]上是减函数,则 的取值范围是_________。
的取值范围是_________。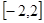 上的奇函数
上的奇函数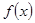 ,它在
,它在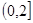 上的图象是一条如右图所示线段(不含点
上的图象是一条如右图所示线段(不含点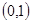 ), 则不等式
), 则不等式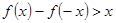 的解集为 .
的解集为 .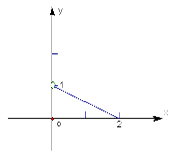
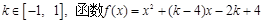 的值恒大于零,则x的取值范围是 .
的值恒大于零,则x的取值范围是 .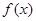 满足
满足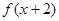 =
= 时,
时,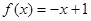 ,则关于
,则关于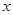 的方程
的方程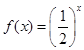 在
在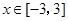 上解的个数是 .
上解的个数是 .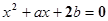 的一根在
的一根在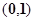 内,另一根在
内,另一根在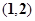 内,则点
内,则点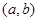 所在区域的面积为
所在区域的面积为