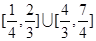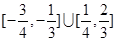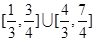题目内容
已知函数f(x)=x2+1,g(x)=f[f(x)],设G(x)=g(x)-λf(x),且G(x)在(-∞,-1]上为减函数,在(-1,0)上为增函数,则实数λ=______.
令t=x2+1,则g(x)=f[f(x)]=t2+1,G(x)=t2-λt+1
当x的范围在(-∞,-1〕和(-1,0)内时,t的范围相应为(2,+∞)和(0,2),
所以,当t在(2,+∞)内为减函数,在(0,2)内为增函数.
要满足此种情况,对称轴x=
=2,
所以入=4,
故答案为:4.
当x的范围在(-∞,-1〕和(-1,0)内时,t的范围相应为(2,+∞)和(0,2),
所以,当t在(2,+∞)内为减函数,在(0,2)内为增函数.
要满足此种情况,对称轴x=
| λ |
| 2 |
所以入=4,
故答案为:4.

练习册系列答案
相关题目
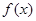 是定义在
是定义在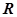 上的奇函数,且
上的奇函数,且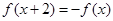 ,若
,若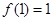 ,则
,则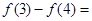 ( )
( )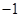
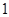
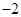
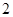
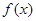 为偶函数,当
为偶函数,当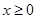 时,
时,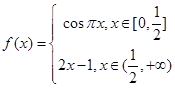 ,则不等式
,则不等式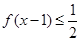 的解集为( )
的解集为( )