题目内容
若实数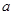 满足
满足 恒成立,则函数
恒成立,则函数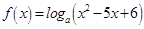 的单调减区间为。
的单调减区间为。
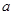 满足
满足 恒成立,则函数
恒成立,则函数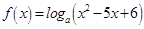 的单调减区间为。
的单调减区间为。
解:令g(y)="|t-1|-|t-2|="
1 t≥2
2t-3 1<y< 2
-1 y<1
则函数的图象如下图,由图可知函数的最大值1
由a>|y-1|-|y-2|(y∈R)恒成立可知a>g(y)max,a>1
函数f(x)=loga(x2-5x+6)的定义域为{x|x>3,或x<2}
令u=x2-5x+6在(-∞,2]上单调递减,在[3,+∞)单调递增
y=logau在(0,+∞)单调递增
由复合函数的单调性可知,函数f(x)在(-∞,2)单调递减
故填写(-∞,2)
1 t≥2
2t-3 1<y< 2
-1 y<1
则函数的图象如下图,由图可知函数的最大值1
由a>|y-1|-|y-2|(y∈R)恒成立可知a>g(y)max,a>1
函数f(x)=loga(x2-5x+6)的定义域为{x|x>3,或x<2}
令u=x2-5x+6在(-∞,2]上单调递减,在[3,+∞)单调递增
y=logau在(0,+∞)单调递增
由复合函数的单调性可知,函数f(x)在(-∞,2)单调递减
故填写(-∞,2)

练习册系列答案
相关题目
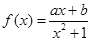 是定义在
是定义在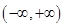 上的奇函数,且
上的奇函数,且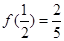 。
。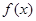 的解析式;
的解析式;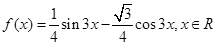
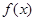 的最小正周期,最大值与最小值.
的最小正周期,最大值与最小值.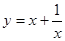 在
在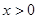 时有 ( )
时有 ( )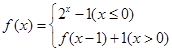 ,则
,则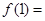 ( )
( )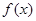 在
在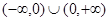 上有意义,且在
上有意义,且在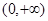 上是增函数,
上是增函数,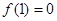
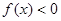 的实数
的实数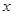 的取值范围;
的取值范围;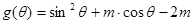 ,若集合
,若集合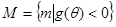 ,集合
,集合 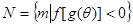 ,求
,求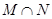
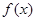 在区间
在区间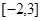 是增函数,则
是增函数,则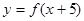 的递增区间是 ( )
的递增区间是 ( )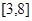
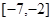

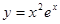 的单调递减区间是. ( )
的单调递减区间是. ( )