题目内容
3.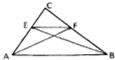 如图直角三角形ABC中,|CA|=|CB|,|AB|=3,点E、F分别在CA、CB上,且EF∥AB,AE=$\sqrt{2}$,则$\overrightarrow{AF}$•$\overrightarrow{BE}$=( )
如图直角三角形ABC中,|CA|=|CB|,|AB|=3,点E、F分别在CA、CB上,且EF∥AB,AE=$\sqrt{2}$,则$\overrightarrow{AF}$•$\overrightarrow{BE}$=( )| A. | 3 | B. | -3 | C. | 0 | D. | -7 |
分析 由题意求得|CA|=|CB|=$\frac{3\sqrt{2}}{2}$,$\overrightarrow{AF}$=$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{BC}$,$\overrightarrow{BE}$=$\overrightarrow{BA}$+$\frac{2}{3}$$\overrightarrow{AC}$,可得$\overrightarrow{AF}$•$\overrightarrow{BE}$=-${\overrightarrow{AB}}^{2}$+$\frac{2}{3}$$\overrightarrow{AB}•\overrightarrow{AC}$-$\frac{2}{3}$$\overrightarrow{AB}•\overrightarrow{BC}$+$\frac{4}{9}$$\overrightarrow{BC}•\overrightarrow{AC}$.再求得$\overrightarrow{BC}•\overrightarrow{AC}$、AB2、$\overrightarrow{AB}•\overrightarrow{AC}$、$\overrightarrow{AB}•\overrightarrow{BC}$的值,从而得到$\overrightarrow{AF}$•$\overrightarrow{BE}$的值.
解答 解: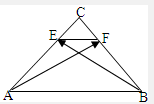 ∵Rt△ABC中,|CA|=|CB|,|AB|=3,
∵Rt△ABC中,|CA|=|CB|,|AB|=3,
∴|CA|2+|CB|2=|AB|2=9,可得|CA|2=|CB|2=$\frac{9}{2}$,|CA|=|CB|=$\frac{3\sqrt{2}}{2}$.
而AC上的点E满足|AE|=$\frac{2}{3}$|AC|.
又∵点E、F分别在CA、CB上,EF∥AB,
∴$\frac{|AE|}{|AC|}$=$\frac{|BF|}{|BC|}$=$\frac{2}{3}$,可得$\overrightarrow{BF}$=$\frac{2}{3}$$\overrightarrow{BC}$,
由此可得$\overrightarrow{AF}$=$\overrightarrow{AB}$+$\overrightarrow{BF}$=$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{BC}$,同理可得$\overrightarrow{BE}$=$\overrightarrow{BA}$+$\frac{2}{3}$$\overrightarrow{AC}$.
∴$\overrightarrow{AF}$•$\overrightarrow{BE}$=($\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{BC}$ )•( $\overrightarrow{BA}$+$\frac{2}{3}$$\overrightarrow{AC}$)=-${\overrightarrow{AB}}^{2}$+$\frac{2}{3}$$\overrightarrow{AB}•\overrightarrow{AC}$-$\frac{2}{3}$$\overrightarrow{AB}•\overrightarrow{BC}$+$\frac{4}{9}$$\overrightarrow{BC}•\overrightarrow{AC}$.
∵BC⊥AC,∠CAB=∠CBA=$\frac{π}{4}$,|AB|=3,|CA|=|CB|=$\frac{3\sqrt{2}}{2}$,
∴$\overrightarrow{BC}•\overrightarrow{AC}$=0,AB2=9,$\overrightarrow{AB}•\overrightarrow{AC}$=3•$\frac{3\sqrt{2}}{2}$cos$\frac{π}{4}$=$\frac{9}{2}$,$\overrightarrow{AB}•\overrightarrow{BC}$=3•$\frac{3\sqrt{2}}{2}$•cos135°=-$\frac{9}{2}$,
∴$\overrightarrow{AF}$•$\overrightarrow{BE}$=-9+$\frac{2}{3}$•$\frac{9}{2}$-$\frac{2}{3}$•(-$\frac{9}{2}$)+0=×0=-3,
故选:B.
点评 本题在等腰直角三角形中求向量的数量积,着重考查了等腰直角三角形的性质、向量的线性运算性质、向量的数量积及其运算性质等知识,属于中档题.

| A. | 这样的三角形不存在 | |
| B. | 这样的三角形存在,且为锐角三角形 | |
| C. | 这样的三角形存在,且为直角三角形 | |
| D. | 这样的三角形存在,且为钝角三角形 |
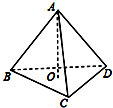 在三棱锥A-BCD中,已知AB⊥CD,BC⊥AD,如图所示,则点A在平面BCD内的射影O是△BCD( )
在三棱锥A-BCD中,已知AB⊥CD,BC⊥AD,如图所示,则点A在平面BCD内的射影O是△BCD( )| A. | 三条中线的交点 | B. | 三角平分线的交点 | ||
| C. | 三条高线的交点 | D. | 三垂直平分线的交点 |
| A. | 141π | B. | 45π | C. | 3$\sqrt{5}$π | D. | 24π |
 如图,△ACB,△ADC都为等腰直角三角形,M、O为AB、AC的中点,且平面ADC⊥平面ACB,AB=4,AC=2$\sqrt{2}$,AD=2.
如图,△ACB,△ADC都为等腰直角三角形,M、O为AB、AC的中点,且平面ADC⊥平面ACB,AB=4,AC=2$\sqrt{2}$,AD=2.