题目内容
18.设点F1(-c,0)、F2(c,0)分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>0)的左、右焦点,P为椭圆C上任意一点,且$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$的最小值为0.(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l1:y=kx+m,l2:y=kx+n(直线l1、l2不重合),若l1、l2均与椭圆C相切,试探究在x轴上是否存在定点Q,使点Q到l1、l2的距离之积恒为1?若存在,请求出点Q坐标;若不存在,请说明理由.
分析 (I)设出P点的坐标,得到$\overrightarrow{{F}_{1}P}$,$\overrightarrow{{F}_{2}P}$的坐标,由$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$最小值为0求出c的值,进而求出a2的值,从而求出椭圆的方程;
(II)分别把l1,l2代入椭圆方程得:m2=1+2k2,n2=1+2k2,从而m+n=0,设在x轴上存在点Q(t,0),点Q到直线l1,l2的距离之积为1,得到:|k2t2-m2|=k2+1,从而求出t的值.
解答 解:(I)设P(x,y),则有$\overrightarrow{{F}_{1}P}$=(x+c,y),$\overrightarrow{{F}_{2}P}$=(x-c,y),
$\overrightarrow{{PF}_{1}}$•$\overrightarrow{{PF}_{2}}$=x2+y2-c2=$\frac{{a}^{2}-1}{{a}^{2}}$x2+1-c2,x∈[-a,a],
由$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$最小值为0得:1-c2=0⇒c=1⇒a2=2,
∴椭圆C的方程为:$\frac{{x}^{2}}{2}$+y2=1;
(II)把l1的方程代入椭圆方程得:(1+2k2)x2+4mkx+2m2-2=0,
∵直线l1与椭圆C相切,∴△=16k2m2-4(1+2k2)(2m2-2)=0,
化简得:m2=1+2k2,
同理可得:n2=1+2k2,
∴m2=n2,若m=n,则l1,l2重合,不合题意,
∴m=-n即m+n=0,
设在x轴上存在点Q(t,0),点Q到直线l1,l2的距离之积为1,
则$\frac{|kt+m|}{\sqrt{{k}^{2}+1}}$-$\frac{|kt-m|}{\sqrt{{k}^{2}+1}}$=1,即:|k2t2-m2|=k2+1,
把1+2k2=m2代入并去绝对值整理,
k2(t2-3)=2或者k2(t2-1)=0
前式显然不恒成立;而要使得后式对任意的k∈R恒成立
则t2-1=0,解得:t=±1;
综上所述,满足题意的定点Q存在,其坐标为(-1,0)或(1,0).
点评 本题考查了求椭圆的标准方程问题,考查了直线和圆锥曲线的关系,是一道中档题.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案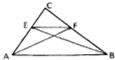 如图直角三角形ABC中,|CA|=|CB|,|AB|=3,点E、F分别在CA、CB上,且EF∥AB,AE=$\sqrt{2}$,则$\overrightarrow{AF}$•$\overrightarrow{BE}$=( )
如图直角三角形ABC中,|CA|=|CB|,|AB|=3,点E、F分别在CA、CB上,且EF∥AB,AE=$\sqrt{2}$,则$\overrightarrow{AF}$•$\overrightarrow{BE}$=( )| A. | 3 | B. | -3 | C. | 0 | D. | -7 |
| A. | [-$\frac{π}{4}$,$\frac{π}{4}$] | B. | [-$\frac{π}{2}$,0] | C. | [-$\frac{5π}{12}$,$\frac{π}{12}$] | D. | [$\frac{π}{12}$,$\frac{7π}{12}$] |
| A. | $\frac{{x}^{2}}{4}-{y}^{2}=1$ | B. | x2-$\frac{{y}^{2}}{4}=1$ | C. | $\frac{{x}^{2}}{10}-\frac{{y}^{2}}{5}=1$ | D. | $\frac{{x}^{2}}{16}-\frac{{y}^{2}}{4}=1$ |