题目内容
1．
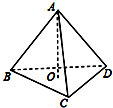在三棱锥A-BCD中，已知AB⊥CD，BC⊥AD，如图所示，则点A在平面BCD内的射影O是△BCD（ ）| A． | 三条中线的交点 | B． | 三角平分线的交点 | ||
| C． | 三条高线的交点 | D． | 三垂直平分线的交点 |
分析 由线面垂直得线线垂直，再由线线垂直得线面垂直，最后得线线垂直，从而得出答案．
解答 解：∵点A在平面BCD内的射影O
∴AO⊥CD，AO⊥BC
又∵AB⊥CD，BC⊥AD
∴CD⊥面ABO，BC⊥面ADO
∴BO⊥CD，DO⊥BC
∴O是△BCD三条高线的交点
故选C．
点评 本小题主要考查空间线面关系、空间想象能力和逻辑推理能力，属于中档题．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
3．
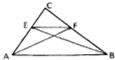如图直角三角形ABC中，|CA|=|CB|，|AB|=3，点E、F分别在CA、CB上，且EF∥AB，AE=$\sqrt{2}$，则$\overrightarrow{AF}$•$\overrightarrow{BE}$=（ ）
如图直角三角形ABC中，|CA|=|CB|，|AB|=3，点E、F分别在CA、CB上，且EF∥AB，AE=$\sqrt{2}$，则$\overrightarrow{AF}$•$\overrightarrow{BE}$=（ ）| A． | 3 | B． | -3 | C． | 0 | D． | -7 |
11．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1，F2，过点F1作直线l⊥x轴交双曲线C的渐近线于点A，B若以AB为直径的圆恰过点F2，则该双曲线的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | $\sqrt{5}$ |