题目内容
11.求函数y=$\frac{a({x}^{2}+3)+x+1}{x+1}$(x>-1)的最值.分析 化简y=$\frac{a({x}^{2}+3)+x+1}{x+1}$=a$\frac{{x}^{2}+3}{x+1}$+1,再令f(x)=$\frac{{x}^{2}+3}{x+1}$=(x+1)+$\frac{4}{x+1}$-2;从而由基本不等式可确定f(x)≥2;再讨论a的正负以确定最值.
解答 解:∵y=$\frac{a({x}^{2}+3)+x+1}{x+1}$=a$\frac{{x}^{2}+3}{x+1}$+1,
∴令f(x)=$\frac{{x}^{2}+3}{x+1}$=(x+1)+$\frac{4}{x+1}$-2;
∵x+1>0,
∴(x+1)+$\frac{4}{x+1}$≥4,
(当且仅当x+1=$\frac{4}{x+1}$时,等号成立);
故f(x)≥2;
故当a>0时,y=$\frac{a({x}^{2}+3)+x+1}{x+1}$=a$\frac{{x}^{2}+3}{x+1}$+1有最小值2a+1;
当a<0时,y=$\frac{a({x}^{2}+3)+x+1}{x+1}$=a$\frac{{x}^{2}+3}{x+1}$+1有最大值2a+1.
点评 本题考查了函数的化简与基本不等式的应用,同时考查了分类讨论的应用,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
19.设命题 p:函数f(x)=ex-1在R上为增函数;命题q:函数f(x)=cos(x+π)为奇函数.则下列命题中真命题是( )
| A. | p∧q | B. | (¬p)∨q | C. | (¬p)∧(¬q) | D. | p∧(¬q) |
3.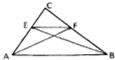 如图直角三角形ABC中,|CA|=|CB|,|AB|=3,点E、F分别在CA、CB上,且EF∥AB,AE=$\sqrt{2}$,则$\overrightarrow{AF}$•$\overrightarrow{BE}$=( )
如图直角三角形ABC中,|CA|=|CB|,|AB|=3,点E、F分别在CA、CB上,且EF∥AB,AE=$\sqrt{2}$,则$\overrightarrow{AF}$•$\overrightarrow{BE}$=( )
 如图直角三角形ABC中,|CA|=|CB|,|AB|=3,点E、F分别在CA、CB上,且EF∥AB,AE=$\sqrt{2}$,则$\overrightarrow{AF}$•$\overrightarrow{BE}$=( )
如图直角三角形ABC中,|CA|=|CB|,|AB|=3,点E、F分别在CA、CB上,且EF∥AB,AE=$\sqrt{2}$,则$\overrightarrow{AF}$•$\overrightarrow{BE}$=( )| A. | 3 | B. | -3 | C. | 0 | D. | -7 |
7.若直线2x+y-2$\sqrt{5}$=0过双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点,且与双曲线的一条渐近线垂直,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{4}-{y}^{2}=1$ | B. | x2-$\frac{{y}^{2}}{4}=1$ | C. | $\frac{{x}^{2}}{10}-\frac{{y}^{2}}{5}=1$ | D. | $\frac{{x}^{2}}{16}-\frac{{y}^{2}}{4}=1$ |