题目内容
8．若三角形三边的高的长度分别为2，3，4，则（ ）| A． | 这样的三角形不存在 | |
| B． | 这样的三角形存在，且为锐角三角形 | |
| C． | 这样的三角形存在，且为直角三角形 | |
| D． | 这样的三角形存在，且为钝角三角形 |
分析 设高2，3，4对应三边分别为a，b，c，根据面积相等求出三边之比，利用余弦定理求出cosA的值小于0，即可做出判断．
解答 解：设高2，3，4对应三边分别为a，b，c，
根据面积相等得：$\frac{1}{2}$a•2=$\frac{1}{2}$b•3=$\frac{1}{2}$c•4，
整理得：2a=3b=4c，即a：b：c=6：4：3，
由余弦定理得：cosA=$\frac{{3}^{2}+{4}^{2}-{6}^{2}}{2×3×4}$=-$\frac{11}{24}$＜0，
∴A为钝角，即△ABC为钝角三角形，
则这样的三角形存在，且为钝角三角形，
故选：D．
点评 此题考查了余弦定理，以及余弦函数的性质，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
19．设命题 p：函数f（x）=ex-1在R上为增函数；命题q：函数f（x）=cos（x+π）为奇函数．则下列命题中真命题是（ ）
| A． | p∧q | B． | （￢p）∨q | C． | （￢p）∧（￢q） | D． | p∧（￢q） |
3．
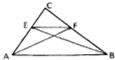如图直角三角形ABC中，|CA|=|CB|，|AB|=3，点E、F分别在CA、CB上，且EF∥AB，AE=$\sqrt{2}$，则$\overrightarrow{AF}$•$\overrightarrow{BE}$=（ ）
如图直角三角形ABC中，|CA|=|CB|，|AB|=3，点E、F分别在CA、CB上，且EF∥AB，AE=$\sqrt{2}$，则$\overrightarrow{AF}$•$\overrightarrow{BE}$=（ ）| A． | 3 | B． | -3 | C． | 0 | D． | -7 |
3．将函数y=sin（2x-$\frac{π}{3}$）的图象向左移动$\frac{π}{3}$个单位，得到函数y=f（x）的图象，则函数y=f（x）的一个单调递增区间是（ ）
| A． | [-$\frac{π}{4}$，$\frac{π}{4}$] | B． | [-$\frac{π}{2}$，0] | C． | [-$\frac{5π}{12}$，$\frac{π}{12}$] | D． | [$\frac{π}{12}$，$\frac{7π}{12}$] |
4．学校开展阳光体育活动，对学生的锻练时间进行随机抽样调查，从中随机抽取男、女生各25名进行了问卷调查，得到了如下列联表：
（Ⅰ） 根据上表数据求x，y，并据此资料分析：有多大的把握可以认为“锻练时间与性别有关”？
（Ⅱ） 从这50名学生中用分层抽样的方法抽取5人为样本，求从该样本中任取2人，
至少有1人锻练时间少于1小时的概率．
K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
| 锻练时间 | 男生 | 女生 | 合计 |
| 少于1小时 | 5 | 15 | 20 |
| 不少于1小时 | 20 | 10 | 30 |
| 合 计 | 25 | 25 | 50 |
（Ⅱ） 从这50名学生中用分层抽样的方法抽取5人为样本，求从该样本中任取2人，
至少有1人锻练时间少于1小时的概率．
K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
| P（K2≥K0） | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |