题目内容
已知f(x)=sin(x+ ),g(x)=cos(x-
),g(x)=cos(x- ),则下列结论中不正确的是
),则下列结论中不正确的是
 ),g(x)=cos(x-
),g(x)=cos(x- ),则下列结论中不正确的是
),则下列结论中不正确的是| A.函数y=f(x)g(x)的最小正周期为π |
B.函数y=f(x)g(x)的最大值为 |
C.函数y=f(x)g(x)的图象关于点( ,0)成中心对称 ,0)成中心对称 |
| D.函数y=f(x)g(x)是奇函数 |
C
解:知f(x)=sin(x+ )=cosx,g(x)=cos(x-
)=cosx,g(x)=cos(x- )=sinx,
)=sinx,
A.函数y=f(x)g(x)的最小正周期为π成立,
B.函数y=f(x)g(x)的最大值为 ,成立
,成立
C.函数y=f(x)g(x)的图象关于点( ,0)成中心对称,不成立
,0)成中心对称,不成立
D.函数y=f(x)g(x)是奇函数成立,故选C
 )=cosx,g(x)=cos(x-
)=cosx,g(x)=cos(x- )=sinx,
)=sinx,A.函数y=f(x)g(x)的最小正周期为π成立,
B.函数y=f(x)g(x)的最大值为
 ,成立
,成立C.函数y=f(x)g(x)的图象关于点(
 ,0)成中心对称,不成立
,0)成中心对称,不成立D.函数y=f(x)g(x)是奇函数成立,故选C

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的 部 分 图 象如 图 所示.
的 部 分 图 象如 图 所示. 的 解 析 式;
的 解 析 式; 中,角
中,角 的 对 边 分 别 是
的 对 边 分 别 是 ,若
,若 的 取 值 范 围.
的 取 值 范 围.
 的图像按向量
的图像按向量 平移后所得函数图像的解析式为( ).
平移后所得函数图像的解析式为( ).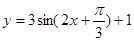



 的导函数
的导函数 的部分图像如图所示:图象与
的部分图像如图所示:图象与 轴交点
轴交点 ,与x轴正半轴的交点为A、C,B为图象的最低点 ,则函数
,与x轴正半轴的交点为A、C,B为图象的最低点 ,则函数


 时,求f(x)的值域.
时,求f(x)的值域.  中,若
中,若 ,求角
,求角 的大小.
的大小. 的图象按向量
的图象按向量 平移后,对应的函数为偶函数,求
平移后,对应的函数为偶函数,求 取最小值时的向量
取最小值时的向量 ,
,
 ,设函数
,设函数 .
. 的值域;
的值域; 的三个内角分别为
的三个内角分别为 ,
, ,
, ,若
,若 ,
, ,求
,求 的值.
的值. 的周期为
的周期为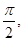
 的单调递增区间;
的单调递增区间; 、
、 、
、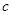 满足
满足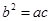 ,且边
,且边 ,求此时函数
,求此时函数 的值为_____________.
的值为_____________.