题目内容
(Ⅰ)在
中,若
,求角
的大小.
(Ⅱ)对于(Ⅰ)中的角,函数
的图象按向量
平移后,对应的函数为偶函数,求
取最小值时的向量.
中,若,求角的大小.(Ⅱ)对于(Ⅰ)中的角
,函数的图象按向量平移后,对应的函数为偶函数,求取最小值时的向量.(Ⅰ) 
. (Ⅱ) 
.
. (Ⅱ) .（1）把三边的关系代入
可得
的值，可求出角；
（2）由（1）得
，平移
个单位后为偶函数，则其对称轴为
轴，所以
，即
.所以的最小值是
..
解：(Ⅰ)∵
,∴
.∵为三角形的内角,∴.
(Ⅱ).设
,则按向量平移后得,
.
当此函数为偶函数时,有,∴.又最小,
∴
,故.
可得的值，可求出角；（2）由（1）得
，平移个单位后为偶函数，则其对称轴为轴，所以，即.所以的最小值是..解：(Ⅰ)∵
,∴.∵为三角形的内角,∴.(Ⅱ)
.设,则按向量平移后得,.当此函数为偶函数时,有
,∴.又最小,∴
,故.
练习册系列答案
相关题目
．
的图象经过怎样的平移和伸缩变换得到？
（其中
的最小正周期为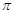
.
的值，并求函数
的单调递减区间；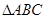
中，
分别是角
的对边，若
，求
的对边长分别为a、b、c，已知a、b、c成等比数列，且
的大小；
，求函数
的值域. 
)，g(x)＝cos(x－
，0)成中心对称
)+sin(
)的图象的相邻两对称轴之间的距离是______.
的图象沿向量
平移后得到函数
的图象，则向量
，
的图像，只需将函数
，
个单位长度
个单位长度
单调增区间为( )
