题目内容
（本小题满分14分）
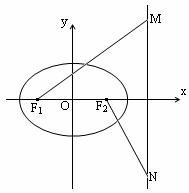
如图，椭圆
（
）的左、右焦点分别为F1（-1，0）、
F2（1，0），M、N是直线
上的两个动点，且
。
（1）设曲线C是以MN为直径的圆，试判断原点O与圆C的位置关系；
（2）若以MN为直径的圆中，最小圆的半径为2
，求椭圆的方程。
（1）设M（
，
）、N（，
），
则
(1+，)，
=（-1，），
∵ 
∴ (1+，)（-1，）=0，
∴ +
=1 ……………………………3分
圆心C（，
），半径
………………………5分
∴ |OC|2=+
，
∴ |OC|2-
= +=1
………………6分
∴ |OC|
∴ 原点O在圆C外 ……………………………7分
（2）∵ +=1 ∴ 
∴ 
=
………9分
∵ 
∴ 
∴ 
1 ∴ -10 …………10分
∴ 
当且仅当
时等号成立 ……12分
∴ 
=2
∴ =3 ………13分
∵ ∴ 
∴ 所求椭圆的方程为
…………………14分
练习册系列答案
相关题目
(a＞b＞0)，曲线C2的方程为y=
，且曲线C1与C2在第一象限内只有一个公共点P。（1）试用a表示点P的坐标；（2）设A、B是椭圆C1的两个焦点，当a变化时，求△ABP的面积函数S(a)的值域；（3）记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积，试求函数f(a)=min{g(a), S(a)}的表达式。
=2，点（
）在函数
的图像上，其中
=
.
}是等比数列；
，求
及数列{
}的通项公式；
，求数列{
}的前n项和
，并证明
.
天(
)的销售价格(单位：元)为
，第
，已知该商品成本为每件25元.
关于第
的图像在点
处的切线与直线
平行.
，
满足的关系式；
上恒成立，求
（
）