题目内容
14．若函数f（x）=|$\frac{{x}^{2}+4x+1}{x}$|-a的图象与x轴恰有四个不同的交点，则实数a的取值范围为（0，2）∪（6，+∞）．分析 由题意可得函数y=|$\frac{{x}^{2}+4x+1}{x}$|=|x+$\frac{1}{x}$+4|的图象和直线y=a有4个交点，数形结合可得a的范围．
解答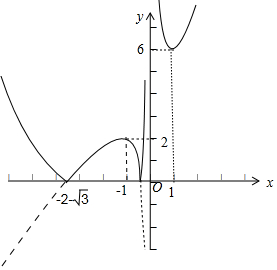 
解：函数f（x）=|$\frac{{x}^{2}+4x+1}{x}$|-a的图象与x轴恰有
四个不同的交点，
即函数y=|$\frac{{x}^{2}+4x+1}{x}$|=|x+$\frac{1}{x}$+4|的图象和直线y=a有
4个交点．
对于 y=|$\frac{{x}^{2}+4x+1}{x}$|=|x+$\frac{1}{x}$+4|=
$\left\{\begin{array}{l}{x+\frac{1}{x}+4，x＞0}\\{x+\frac{1}{x}+4，x∈（-2-\sqrt{3}，-2+\sqrt{3}）}\\{-x-\frac{1}{x}-4，x≤-2-\sqrt{3}或-2+\sqrt{3}≤x＜0}\end{array}\right.$．
如图所示：
则实数a∈（0，2）∪（6，+∞），
故答案为：（0，2）∪（6，+∞）．
点评 函数的零点与方程的根的关系，方程根的存在性以及个数判断，体现了数形结合、转化的数学思想，属于中档题．
练习册系列答案
相关题目
2．已知集合P={x|x2-2x≥0}，Q={x|1＜x≤2}，则P∩（∁RQ）=（ ）
| A． | （-∞，0]∪[2，+∞） | B． | （-∞，0]∪（2，+∞） | C． | （-∞，0）∪[2，+∞） | D． | （-∞，0）∪（2，+∞） |
19．“α=$\frac{π}{6}$”是“tan2α=$\sqrt{3}$”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
3．下列函数中，既为奇函数又在（0，+∞）内单调递减的是（ ）
| A． | f（x）=x3 | B． | f（x）=${x}^{-\frac{1}{2}}$ | C． | f（x）=-x | D． | f（x）=x+$\frac{3}{x}$ |