题目内容
15.用0、1、2、3、4这五个数字,可以组成多少个满足下列条件的整数?(Ⅰ)所有的四位数;
(Ⅱ)比21000大的没有重复的五位数.
分析 (Ⅰ)根据题意,先分析首位数字,由于首位数字不能为0,有4种情况,再分析其他的数位,在剩下的4个数字中任选3个,安排在其他3个数位上;由分步计数原理计算可得答案;
(Ⅱ)根据题意,分2种情况讨论:①、首位数字为3或4时,②、首位数字为2时,分别求出每种情况下的五位数的数目,由分类计数原理计算可得答案.
解答 解:(Ⅰ)根据题意,要用0、1、2、3、4组成四位数,
则首位数字不能为0,有4种情况,
在剩下的4个数字中任选3个,安排在其他3个数位上,有A43=24种情况,
则一共有4×24=96个四位数;
(Ⅱ)根据题意,要求“21000大的没有重复的五位数”的数目,分2种情况讨论:
①、首位数字为3或4时,将剩下的4个数字进行全排列,安排在其他4个数位上,有A44=24种情况,
则首位数字为3或4时,有2×24=48个符合要求的五位数;
②、首位数字为2时,第二位数字必须是1、3、4中1个,有3种情况,
将剩下的3个数字进行全排列,安排在其他3个数位上,有A33=6种情况,
则首位为2时,有3×6=18个符合要求的五位数;
则共有48+18=66个比21000大的没有重复的五位数.
点评 本题考查排列、组合的运用,把排列问题包含在数字问题中,解题的关键是看清题目的实质,注意数字0的限制.

练习册系列答案
相关题目
5.设F1、F2,分别是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,若双曲线右支上存在一点M,使|OF1|=|OM|,O为坐标原点,且|MF1|=$\sqrt{2}$|MF2|,则该双曲线的离心率为( )
| A. | $\frac{\sqrt{3}+1}{2}$ | B. | $\sqrt{3}+1$ | C. | $\frac{\sqrt{3}+\sqrt{6}}{2}$ | D. | $\sqrt{3}+\sqrt{6}$ |
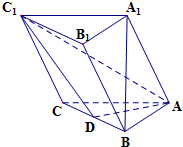 如图,在三棱柱ABC-A1B1C1中,D为棱BC的中点,AB⊥BC,BC⊥BB1,AB=A1B=1,BB1=$\sqrt{2}$.求证:
如图,在三棱柱ABC-A1B1C1中,D为棱BC的中点,AB⊥BC,BC⊥BB1,AB=A1B=1,BB1=$\sqrt{2}$.求证: