题目内容
5．设F1、F2，分别是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点，若双曲线右支上存在一点M，使|OF1|=|OM|，O为坐标原点，且|MF1|=$\sqrt{2}$|MF2|，则该双曲线的离心率为（ ）| A． | $\frac{\sqrt{3}+1}{2}$ | B． | $\sqrt{3}+1$ | C． | $\frac{\sqrt{3}+\sqrt{6}}{2}$ | D． | $\sqrt{3}+\sqrt{6}$ |
分析 依题意可知|OF1|=|OF2|=|OP|判断出∠F1PF2=90°，设出|PF2|=t，则|F1P|=$\sqrt{2}$t，进而利用双曲线定义可用t表示出a，根据勾股定理求得t和c的关系，最后可求得双曲线的离心率．
解答 解：∵|OF1|=|OF2|=|OM|
∴∠F1MF2=90°
设|MF2|=t，则|F1M|=$\sqrt{2}$t，a=$\frac{\sqrt{2}t-t}{2}$
∴t2+2t2=4c2，
∴t=$\frac{2}{\sqrt{3}}$c
∴e=$\frac{c}{a}$=$\sqrt{3}$+$\sqrt{6}$．
故选：D．
点评 本题主要考查了双曲线的简单性质，考查了学生对双曲线定义的理解和灵活运用，属于基础题．
练习册系列答案
相关题目
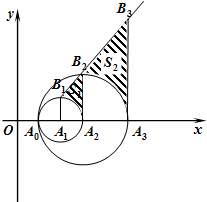如图，在平面直角坐标系xOy中，设a1=2，有一组圆心在x轴正半轴上的圆An（n=1，2，…）与x轴的交点分别为A0（1，0）和An+1（an+1，0）．过圆心An作垂直于x轴的直线ln，在第一象限与圆An交于点Bn（an，bn）．
如图，矩形纸片ABCD的周长为l，面积为S．