题目内容
将正整数1,2,3,4,…,n2(n≥2)任意排成n行n列的数表.对于某一个数表,计算各行和各列中的任意两个数a,b(a>b)的比值
,称这些比值中的最小值为这个数表的“特征值”.则当n=2时,数表的所有可能的特征值中最大值是 .
| a | b |
考点:特征值与特征向量的计算
专题:选作题
分析:可设1在第一行第一列,考虑与1同行或同列的两个数的可能,可得特征值,比较后可得答案.
解答:解:当n=2时,这4个数分别为1、2、3、4,排成了两行两列的数表,
当1、2同行或同列时,这个数表的“特征值”为
;
当1、3同行或同列时,这个数表的特征值分别为
或
;
当1、4同行或同列时,这个数表的“特征值”为
或
,
故这些可能的“特征值”的最大值为
.
故答案为:
.
当1、2同行或同列时,这个数表的“特征值”为
| 4 |
| 3 |
当1、3同行或同列时,这个数表的特征值分别为
| 4 |
| 3 |
| 3 |
| 2 |
当1、4同行或同列时,这个数表的“特征值”为
| 4 |
| 3 |
| 3 |
| 2 |
故这些可能的“特征值”的最大值为
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题考查类比推理和归纳推理,属基础题.

练习册系列答案
相关题目
设i是虚数单位,复数i3+
=( )
| 2i |
| 1+i |
| A、-i | B、i | C、-1 | D、1 |
矩阵A=
,向量
=
,则A10
=( )
|
| α |
|
| α |
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
在极坐标系中,点F(1,0)到直线θ=
(ρ∈R)的距离是( )
| π |
| 4 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
 已知,在Rt△ABC中,CD为斜边上的高,CE平分∠BCD,交AB于点E.求证:AE2=AD•AB.
已知,在Rt△ABC中,CD为斜边上的高,CE平分∠BCD,交AB于点E.求证:AE2=AD•AB.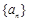 的首项为
的首项为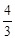 ,公比为
,公比为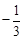 ,其前
,其前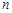 项和记为
项和记为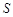 ,又设
,又设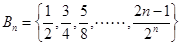
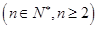 ,
,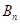 的所有非空子集中的最小元素的和为
的所有非空子集中的最小元素的和为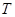 ,则
,则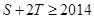 的最小正整数
的最小正整数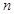 为 .
为 .