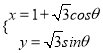题目内容
【题目】已知⊙C：x2＋y2＋2x－4y＋1＝0.
(1)若⊙C的切线在x轴、y轴上截距相等，求切线的方程．
(2)从圆外一点P(x0，y0)向圆引切线PM，M为切点，O为原点，若|PM|＝|PO|，求使|PM|最小的P点坐标．
【答案】（1）切线方程为：y＝0，y＝x，x＋y＝1＋2和x＋y＝1－2.（2）
【解析】
试题分析：⊙C：(x＋1)2＋(y－2)2＝4，圆心C(－1,2)，半径r＝2.
(1)若切线过原点设为y＝kx，则
＝2，∴k＝0或.
若切线不过原点，设为x＋y＝a，则＝2，∴a＝1±2，
∴切线方程为：y＝0，y＝x，x＋y＝1＋2和x＋y＝1－2.·· 7分
(2) 
＝
∴2x0－4y0＋1＝0，
|PM|＝＝
∵P在⊙C外，∴(x0＋1)2＋(y0－2)2>4，将x0＝2y0－代入得5y2－2y0＋>0，
∴|PM|min＝.此时P. 14分
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
【题目】《国务院关于修改〈中华人民共和国个人所得税法实施条例〉的决定》已于2008年3月1日起施行，个人所得税税率表如下：
级数 | 全月应纳税所得额 | 税率 |
1 | 不超过500元的部分 | 5% |
2 | 超过500至2 000元的部分 | 10% |
3 | 超过2 000元至5 000元的部分 | 15% |
… | … | … |
9 | 超过100 000元的部分 | 45% |
注：本表所示全月应纳税所得额为每月收入额减去2 000元后的余额.
(1)若某人2008年4月份的收入额为4 200元，求该人本月应纳税所得额和应纳的税费；
(2)设个人的月收入额为x元，应纳的税费为y元.当0<x≤3 600时，试写出y关于x的函数关系式.
