题目内容
【题目】已知三个点A(2,1),B(3,2),D(-1,4).
(1)求证:![]() ⊥
⊥![]() ;
;
(2)要使四边形ABCD为矩形,求点C的坐标,并求矩形ABCD两对角线所夹锐角的余弦值.
【答案】(1)证明见解析;(2)![]() ,余弦值
,余弦值![]() .
.
【解析】
试题(1)因为已知A(2,1),B(3,2),D(-1,4),可结合问题,联系向量的坐标及垂直的性质,进行证明.
(2)由题先设出C(x, y),再借助![]() =
=![]() ,建立方程可得C点坐标.由点C的坐标,分别表示出所需的向量:
,建立方程可得C点坐标.由点C的坐标,分别表示出所需的向量:![]() =(-2,4),
=(-2,4),![]() =(-4,2),借助向量的数量积的定义,可求出cosθ.
=(-4,2),借助向量的数量积的定义,可求出cosθ.
试题解析:(1)、![]()
![]() ,
,![]()
![]() ⊥
⊥![]() ;
;
(2)、设C(x,y),![]() =(x+1,y-4) ,由
=(x+1,y-4) ,由![]() =
=![]() ,得x=0,y=5,
,得x=0,y=5,![]() C(0,5),
C(0,5),
设矩形ABCD两对角线AC,BD所夹锐角为θ,
![]() =(-2,4),
=(-2,4),![]() =(-4,2),
=(-4,2),![]() =2
=2![]() ,
,![]() =2
=2![]() ,
,
cosθ= =
=![]()

练习册系列答案
相关题目
【题目】某连锁餐厅新店开业打算举办一次食品交易会,招待新老顾客试吃项目经理通过查阅最近5次食品交易会参会人数x(万人)与餐厅所用原材料数量y(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数(万人) | 13 | 9 | 8 | 10 | 12 |
原材料(袋) | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出y关于x的线性回归方程![]()
(2)已知购买原材料的费用C(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有13万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料才能获得最大利润,最大利润是多少?(注:利润L=销售收入-原材料费用)
,投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有13万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料才能获得最大利润,最大利润是多少?(注:利润L=销售收入-原材料费用)
参考公式: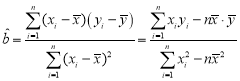 ,
,![]()
参考数据:![]() .
.